Нестационарные процессы в электрических цепях, страница 21

Переход от изображения к оригиналу позволяет заменить интегро-дифференциальные уравнения для оригинала алгебраическими уравнениями для изображения. Это значительно упрощает решение системы уравнений и вычисление изображения искомой функции. Остается только по изображению найти саму функцию, то есть оригинал.

Переход от оригинала к изображению осуществляется с помощью прямого преобразования Лапласа:

.

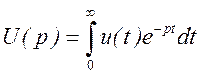Обратный переход от изображения к оригиналу осуществляют на основании обратного преобразования Лапласа:

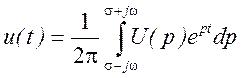
Функция p=σ+jω называется оператором преобразования. В виду того, что оператор р включает в свой состав вещественную и комплексную составляющие, преобразования Лапласа возможны для более широкого класса функций, чем преобразования Фурье. Напомним некоторые свойства преобразования Лапласа:

·  Свойство линейности. Если

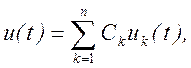 то

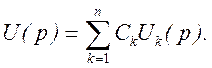
·  Дифференцирование оригинала. Если

 то

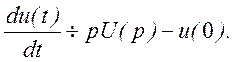
В общем случае

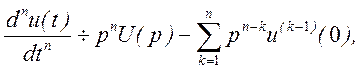
где u^(k-1)(0)- значение производной (к-1)-го порядка функции u(t) при t=0.

·  3. Интегрирование оригинала. Если

u(t)=U(p), то

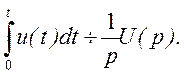
·   Теорема запаздывания. Если u(t) ÷U(р), то

u(t-τ)÷е^-ptU(p)

·  Теорема смещения. Если u(t) ÷U(р), то

U(p±λ)÷u(t)e-λt.

·  Умножение изображений (теорема свертывания). Если u₁(t) ÷U₁(р), u₂(t) ÷U₂(р),то

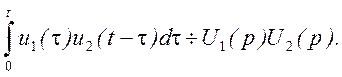
·  Теорема разложения. Еcли изображение имеет вид рациональной дроби

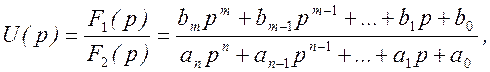
причем степень многочлена F₁(р)  ниже степени многочлена F₂(р) (m<n) коэффициенты a_k и b_k - вещественные числа, а корни p_k уравнения  F₂(p)=0 различны, то оригинал определяется выражением:

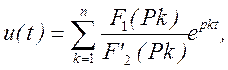
где 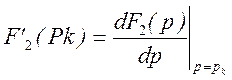 - производная от функции F₂(р) при условии p=p_k.

В случае, если уравнение F₂(р)=0 имеет кратные корни кратности m, то оригинал находится по формуле:

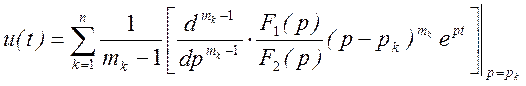
Теорема разложения в сочетании с другими свойствами преобразования Лапласа дает возможность составлять формулы преобразований изображений в оригиналы и наоборот. Основные формулы преобразований, широко используемые в расчетах, приведены в таблице 4.1.

            Таблица 4.1

Ном. n\n		u(t)
11.	1	δ(t)
22.		1(t)
33.		t
44.
55.		e-αt
66.		te-αt
77.
88.
99.		cosωt
110.
111.

Следует отметить, что возможность решения линейных дифференциальных уравнений с помощью операторного метода впервые была показана русским математиком М.Е.Ващенко-Захарченко в 1862г. В конце XIX века английский ученый О.Хевисайд применил этот метод к расчёту электромагнитных переходных процессов. Большой вклад в развитие операционного исчисления и его применение к расчету электромагнитных процессов внесли советские ученые В.С.Игнатовский, A.M.Данилевский, А.М.Зфрос, К.А.Круг, М.И.Канторович и др.

4.1.2. Законы Ома и Кирхгофа в операторной форме

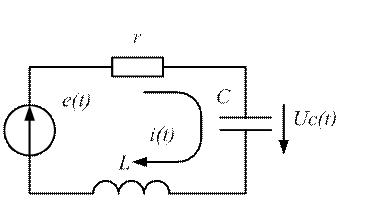
Рис. 4.1

Закон Ома в операторной форме рассмотрим на примере последовательного колебательного контура, на который воздействует ЭДС  при ненулевых начальных условиях. На основании второго закона Кирхгофа для мгновенных значений электрических величин в рассматриваемой цепи можно записать уравнение электрического равновесия:

u_r(t)+ u_l(t)+ u_c(t)=e(t).

Или, раскрыв значения напряжений через общий ток i(t)

.

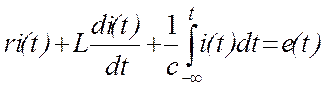Нижний предел у интеграла, описывающего напряжение u_с(t) взят для того, чтобы учесть тот факт, что до момента подключения к цепи источника ЭДС е(t) емкость была заряжена. Следовательно, напряжение на емкости можно представить в виде:

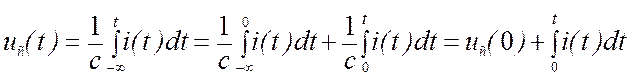
Применим к интегро-дифференциальному уравнению преобразования Лапласа. Будем считать, что заданная ЭДС e(t) и искомый ток i(t) имеют изображения:

i(t)÷I(p); e(t)÷E(p)

На основании свойства линейности преобразования Лапласа, а также теорем дифференцирования и интегрирования можно записать изображения для слагаемых уравнения:

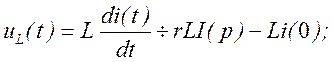
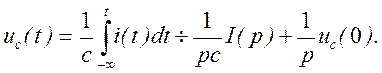
Таким образом, уравнение в операторной форме можно записать следующим образом:

.

Это уравнение является выражением второго закона Кирхгофа в операторной форме для цепи при ненулевых начальных условиях. Перепишем уравнение, объединив слагаемые

.

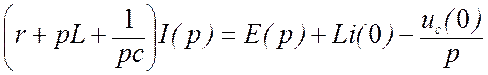Введем обозначения:

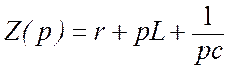 - полное операторное сопротивление:

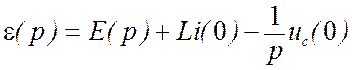 - обобщенная операторная ЭДС.

Обобщенная операторная ЭДС ε(р) учитывает ненулевые начальные условия в цепи: токи в индуктивностях и напряжения на емкостях. Следует отметить, что при нулевых начальных условиях ε(р)=Е(р). Используя введенные соотношения, можно записать:

.

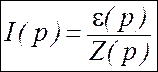Это выражение является законом Ома в операторной форме.

Запишем первый закон Кирхгофа. Для мгновенных значений токов, сходящихся в узле, имеет место соотношение:

.

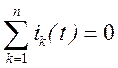Применяя к этому выражению теорему линейности преобразования Лапласа, получим уравнение первого закона Кирхгофа в операторной форме:

.

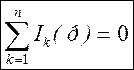Аналогично из выражения второго закона Кирхгофа для любого контура электрической цепи

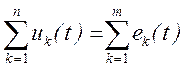
получим выражение этого закона в операторной форме:

,

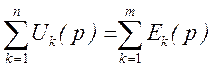где      

Это выражение можно представить и в другой форме

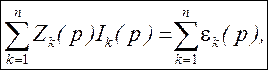
где       .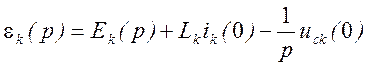

4.1.3. Порядок расчета цепей с помощью эквивалентных операторных схем

Обобщая метод, примененный для получения законов Ома и Кирхгофа в операторной форме, можно предложить следующий алгоритм расчета переходных процессов в цепи:

Определить начальные условия.

Составить систему дифференциальных уравнений для цепи после коммутации, используя любой известный метод расчета цепей.

Перейти от дифференциальных уравнений к изображениям.