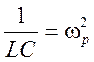 ;
; 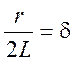 ;
;
![]() .
.
Учитывая эти обозначения, запишем выражение для ![]() и
и ![]() :
:
![]()
![]() ;
; ![]() .
.
Проанализируем, какой вид приобретут в этом случае выражения
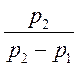 и
и 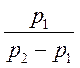 (рис.2.20):
(рис.2.20):
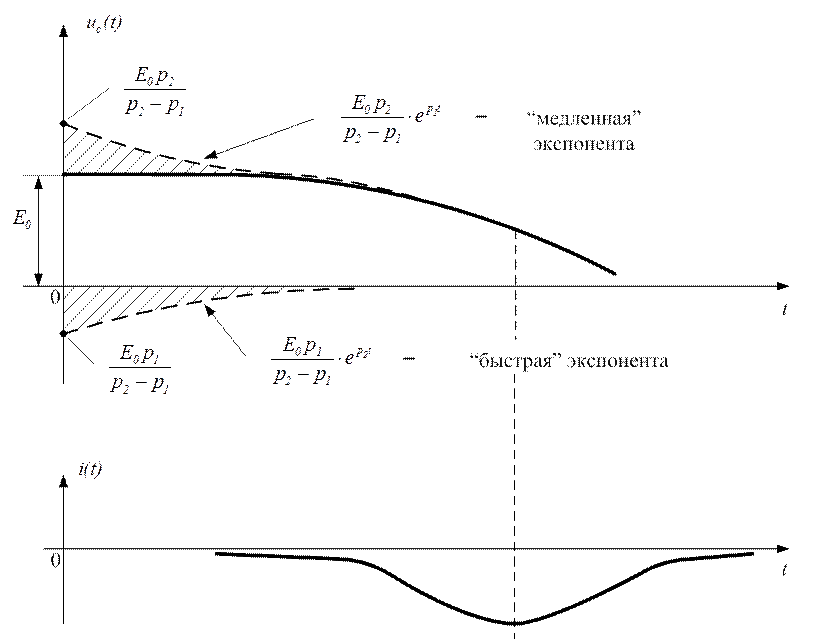
Рис.2.20
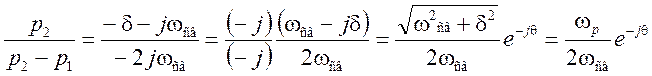 ,
,
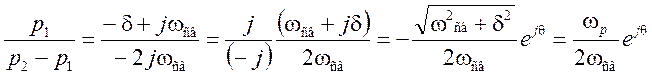 ,
,
где 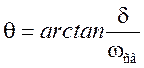 .
.
С учётом полученных выражений, формула для ![]() приобретет вид:
приобретет вид:
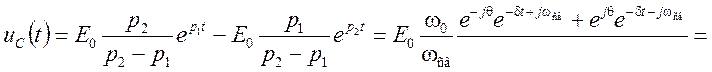
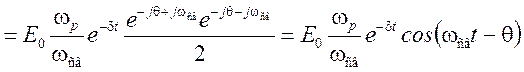 .
.
Для контуров с высокой добротностью ![]() ,
поэтому
,
поэтому ![]() и
и ![]() ,
следовательно
,
следовательно
![]() ,
,
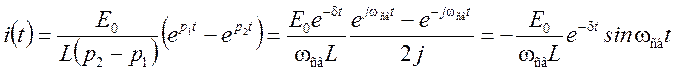 .
.
Графики функций ![]() и
и ![]() приведены на рисунке 2.21
приведены на рисунке 2.21

Рис.2.21
· Свободные процессы в контуре представляют собой затухающие колебания.
·
Длительность затухающих колебаний определяется множителем ![]() и зависит от
и зависит от ![]() и
и
![]() , т.к.
, т.к. 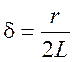
·
Частота колебаний зависит от параметров ![]() и
и ![]() .
.
Для оценки скорости затухания используют:
- декремент затухания - число, показывающее во сколько раз уменьшается амплитуда колебаний за один период:
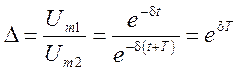 , где
, где 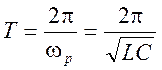 ,
,
![]() -логарифмический декремент
затухания:
-логарифмический декремент
затухания: 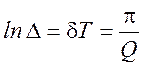
2.6.2. Переходные процессы в цепях второго порядка при подключении к источнику постоянной э.д.с.
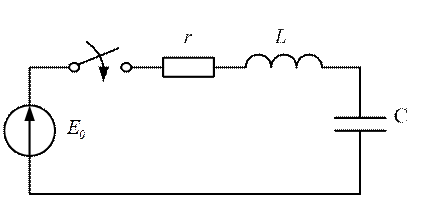
Рис. 2.22
Физическая сущность процессов в этой цепи (рис. 2.22)
заключается в заряде емкости до величины ![]() .
.
В рассматриваемом случае принужденная составляющая
напряжения на емкости ![]() . В общем случае
. В общем случае ![]() . Закон изменения
. Закон изменения ![]() был получен при рассмотрении
свободных процессов в таком контуре.
был получен при рассмотрении
свободных процессов в таком контуре.
Учитывая начальные условия ![]() и
и
![]() можно записать
можно записать
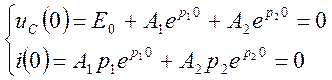
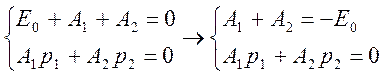
Постоянные интегрирования равны:
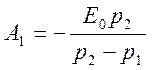
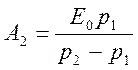 .
.
Корни ![]() и
и ![]() будут такими же, как и для свободных
процессов, а постоянные интегрирования -
противоположны по знаку, поэтому можно записать:
будут такими же, как и для свободных
процессов, а постоянные интегрирования -
противоположны по знаку, поэтому можно записать: ![]() .
.
В предыдущем случае были получены выражения для
апериодического разряда емкости: 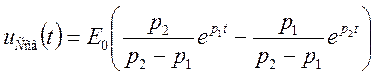 ,
,
и для колебательного разряда емкости: ![]() .
.
Подставляя эти выражения, получим выражения для апериодического заряда
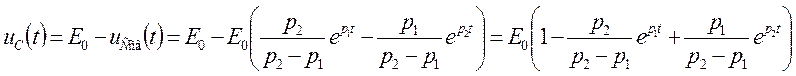 и для колебательного заряда емкости
и для колебательного заряда емкости
![]() .
.
Графики ![]() приведены на
рисунке 2.23
приведены на
рисунке 2.23
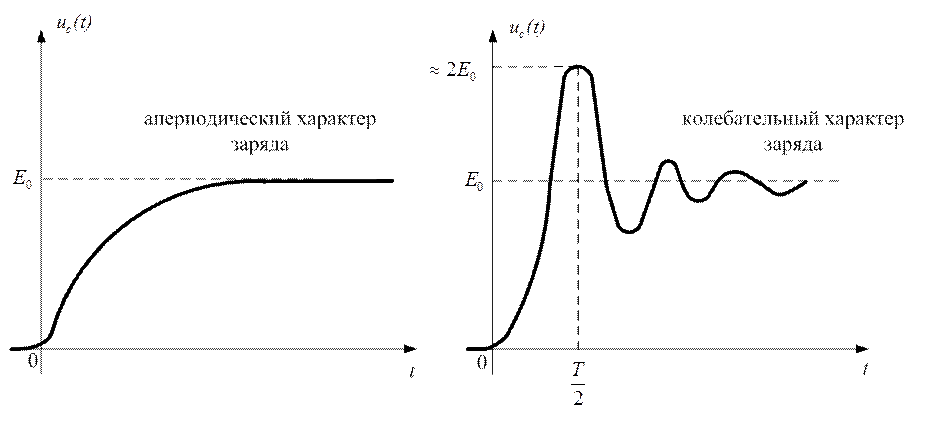
Рис.2.23
Из приведенного графика видно, что в момент времени ![]()
![]() , т.к.
, т.к. ![]() и
и
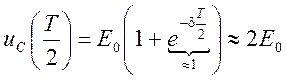 .
.
2.6.3. Переходные процессы в цепях второго порядка при подключении к источнику синусоидальной э.д.с.
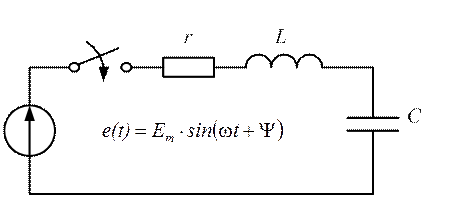
Рис. 2.24
На практике представляют интерес процессы, возникающие в
контуре (рис. 2.24), добротность которого высока ![]() ,
в тех случаях, когда резонансная частота контура
,
в тех случаях, когда резонансная частота контура ![]() равна
частоте синусоидальной э.д.с.
равна
частоте синусоидальной э.д.с. ![]() , а также когда
эти частоты не равны
, а также когда
эти частоты не равны ![]() .
.
В общем случае свободная составляющая напряжения на емкости будет равна:
![]() , если
, если ![]() , то
, то
![]() , т.к.
, т.к. ![]() .
.
Принужденную ![]() составляющую
можно найти следующим образом:
составляющую
можно найти следующим образом: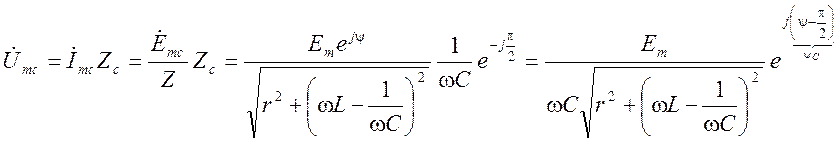 , где
, где 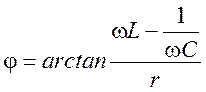 ,
,
![]() .
.
Общее решение будет иметь вид:
![]() .
.
1. Пусть ![]() .
.
Учитывая, что напряжение на емкости в начальный момент
времени равно нулю, найдем постоянную интегрирования ![]() следующим
образом:
следующим
образом:
- изобразим график принужденной составляющей на верхнем графике (рис. 2.25),
- изобразим график
свободной составляющей на нижнем графике (рис. 2.25) так, чтобы в
первоначальный момент времени ![]()
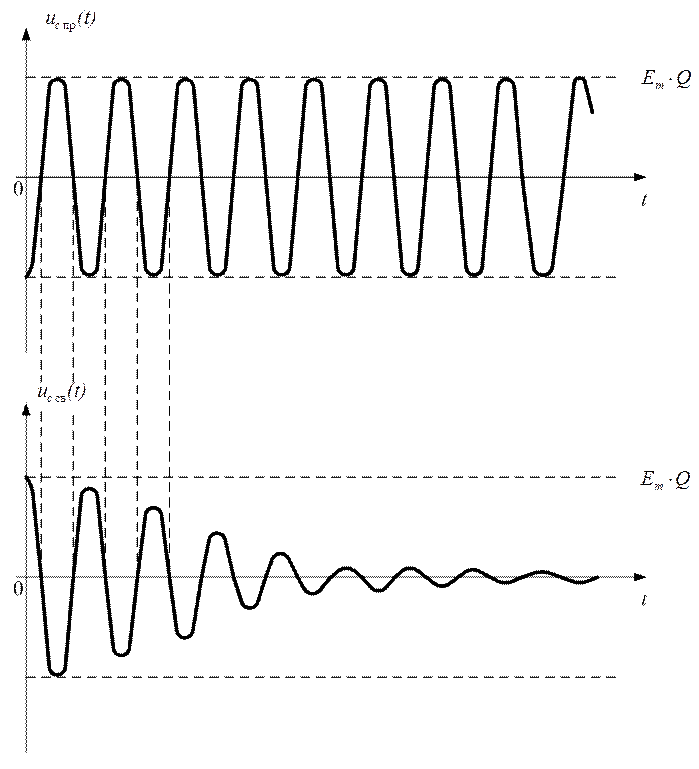
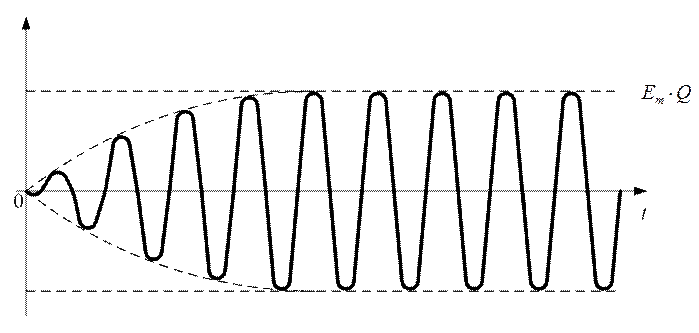
Рис. 2.25
График принужденной составляющей будет иметь амплитуду ![]() , т.к.
, т.к. ![]() ,
т.е. в цепи после окончания переходных процессов будет иметь место резонанс
напряжений. В начальный момент времени напряжение принужденной составляющей
будет начинаться с "
,
т.е. в цепи после окончания переходных процессов будет иметь место резонанс
напряжений. В начальный момент времени напряжение принужденной составляющей
будет начинаться с "![]() ", т.к. напряжение
на емкости при резонансе отстает на
", т.к. напряжение
на емкости при резонансе отстает на ![]() от приложенного
напряжения.
от приложенного
напряжения.
График свободной составляющей будет начинаться с "![]() " т.к. в этот момент времени
свободная составляющая должна скомпенсировать принужденную составляющую, т.к.
" т.к. в этот момент времени
свободная составляющая должна скомпенсировать принужденную составляющую, т.к. ![]() .
.
Таким образом, если ![]() , то при подключении контура к
источнику
, то при подключении контура к
источнику ![]() , напряжение на емкости будет равно
, напряжение на емкости будет равно
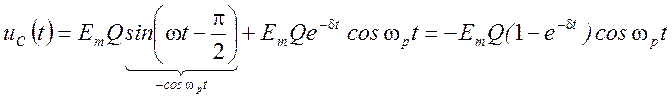 .
.
Аналогично можно показать, что закон нарастания колебаний тока в контуре будет
![]() , где
, где 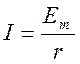 .
.
График напряжения на емкости для рассматриваемого случая ![]() получившего названия изохронизма,
показан на рисунке 2.23
получившего названия изохронизма,
показан на рисунке 2.23

Рис. 2.26
Амплитуда напряжения на емкости нарастает по закону ![]() асимптотически приближаясь к
значению, равному амплитуде этого напряжения при резонансе. Длительность
переходного процесса определяется коэффициентом затухания
асимптотически приближаясь к
значению, равному амплитуде этого напряжения при резонансе. Длительность
переходного процесса определяется коэффициентом затухания ![]() .
.
Чем больше ![]() , тем быстрее
заканчивается переходной процесс. Так как
, тем быстрее
заканчивается переходной процесс. Так как
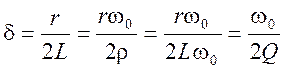 , т.е. чем больше
, т.е. чем больше ![]() , тем меньше
, тем меньше ![]() и
следовательно, больше длительность переходного процесса в контуре.
и
следовательно, больше длительность переходного процесса в контуре.
2. Пусть ![]() .
.
В случае, когда частота источника э.д.с не совпадает с частотой свободных колебаний в контуре, напряжение на емкости будет представлять собой суммы двух колебаний с разными частотами, амплитуда одного из которых убывает по экспоненциальному закону. При этом возникающие так называемые биения (см. рис. 2.27)

Рис.2.27
2.7. Применение цепей второго порядка в РЭТ
Цепи второго порядка широко используются на практике в современной радиоэлектронной технике.
2.7.1. Применение цепи второго порядка в импульсном модуляторе РЛС с полным разрядом накопительной емкости
Ранее были рассмотрены переходные процессы в импульсном модуляторе РЛС с частичным разрядом ёмкости. В мощных РЛС чаще применяют схемы с полным разрядом накопительной ёмкости. Такие схемы позволяют создавать более мощные импульсы (см. рис. 2.28)
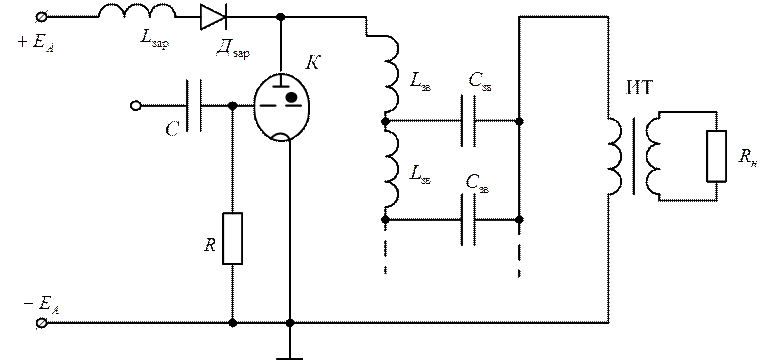
Рис.2.28
На данной схеме обозначены:
![]() - зарядный дроссель;
- зарядный дроссель;![]() - фиксирующий диод;
- фиксирующий диод; ![]() - формирующая линия, состоящая из нескольких
звеньев;
- формирующая линия, состоящая из нескольких
звеньев; ![]() -
звено формирующей линии;
-
звено формирующей линии; ![]() - импульсный трансформатор;
- импульсный трансформатор; ![]() -
нагрузка-генератор СВЧ;
-
нагрузка-генератор СВЧ; ![]() - управляемый электронный ключ-тиратрон.
- управляемый электронный ключ-тиратрон.
Эквивалентная схема заряда накопительных емкостей звеньев приведена на рисунке 2.29
 В начальный момент времени в такой цепи имеют место
нулевые начальные условия:
В начальный момент времени в такой цепи имеют место
нулевые начальные условия: ![]() ,
, ![]() .
.
Рис. 2.29
При подключении источника постоянной э.д.с. в цепи может
происходить колебательный заряд суммарной накопительной емкости
(индуктивностями звеньев ![]() ,
и обмотки
,
и обмотки ![]() можно пренебречь).
можно пренебречь).
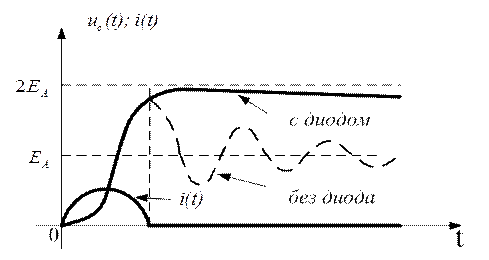
Рис. 2.30
Наличие в цепи фиксирующего диода предотвращает возникновение колебаний напряжения на емкостях формирующей линии. Эпюры напряжений приведены на рисунке 2.30.
Следует отметить, что запас энергии в емкостях формирующей
линии в 4 раза больше, чем в модуляторах с частичным разрядом емкости. Полагая
накопительные ёмкости одинаковыми, считаем, что запас энергии в модуляторе с
частичным зарядом ![]() , а запас энергии в
модуляторе с полным разрядом
, а запас энергии в
модуляторе с полным разрядом 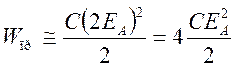 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.