Часть этих сигналов поступает непосредственно на сумматор, остальные (в соответствии с кодом сигнала) - сначала на фазоинверторы, а затем уже на сумматор. В фазоинверторе начальные фазы всех парциальных импульсов меняются на противоположные.
В сумматоре происходит сложение поступающих на его вход сигналов. Суммарный сигнал поступает далее на вход фильтра Ф, а с него - на выход устройства.
Процессы, происходящие в рассматриваемом устройстве, иллюстрируются на рисунке 3.10. Здесь показаны графики сигналов, формируемых на входах и выходе сумматора и выходе фильтра Ф. Как видно из этого рисунка, сигнал, снимаемых с выхода сумматора, представляет собой несколько одиночных радиоимпульсов, длительность парциальных импульсов входного сигнала. Амплитуды всех этих импульсов, кроме центрального равны амплитуде входного сигнала. Амплитуда же центрального импульса оказалась в N раз больше, чем амплитуда входного сигнала. Если этот центральный импульс считать основным выходным сигналом сумматора, то действительно можно говорить о том, что произошло сжатие во времени входного сигнала в N раз. Но эффект сжатия сопровождается размножением сжатого сигнала, в результате которого основной (центральный) импульс приобрел симметрично расположенные во времени боковые «спутники», которые обычно называют боковыми лепестками или остатками.
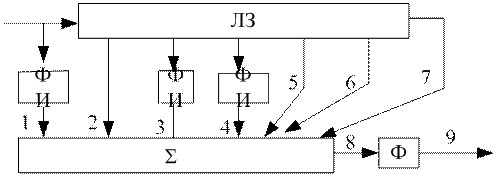
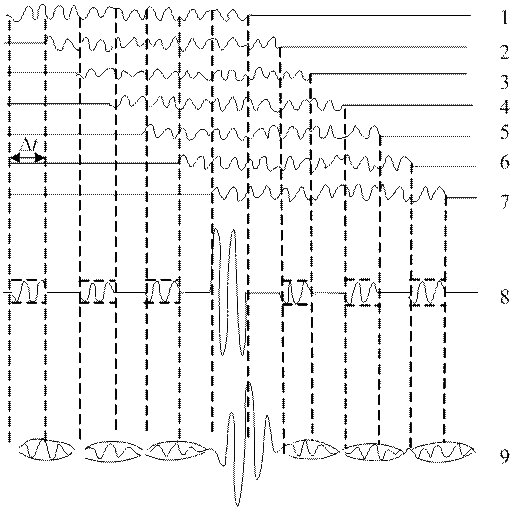
Рис.3.10
Импульсы с выхода сумматора поступают на вход фильтра, параметры которого оказываются согласованными с параметрами этих импульсов. В фильтре входные прямоугольные радиоимпульсы преобразуются в треугольнике. Очевидно, первым грубым приближением такого фильтра является одиночный колебательный контур, постоянная времени τ которого равна длительности парциальных импульсов. В этом случае, как известно, выходной сигнал контура имеет почти треугольную форму.
По рассмотренной схеме можно реализовать согласованные фильтры и для других видов сигналов.
3.5. Влияние ограниченности полосы пропускания цепи и неравномерности ее АЧХ на форму выходных сигналов
3.5.1. Влияние ограниченности полосы пропускания цепи на форму передаваемых сигналов
Все реальные цепи имеют ограниченные полосы пропускания. При этом у некоторых из них в пределах полосы пропускания АЧХ равномерна (например, LC-фильтры, индуктивно-связанные контуры), у других (одиночные колебательные контуры, интегрирующие и дифференцирующие цепи и т.д.) - неравномерна. Поэтому при анализе
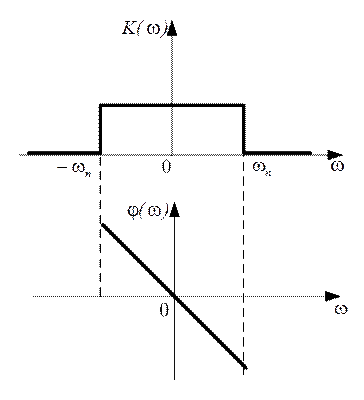
искажений сигналов, проходящих по этим цепям, рассматривают обычно отдельно влияние ограниченности полосы пропускания и неравномерности АЧХ на форму выходных сигналов цепи. Предположим, что цепь имеет следующий комплексный коэффициент передачи
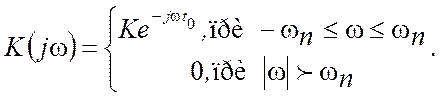
Рис. 3.11
Соответствующие этому комплексному коэффициенту передачи, частотные характеристики цепи показаны на рисунке.
Такие характеристики имеют идеальные фильтры нижних частот. Пусть на вход такого фильтра воздействует сигнал вида
.
Реакция цепи на такой сигнал, как известно, является импульсной характеристикой цепи H(t). Определим ее, отыскав спектральную плотность выходного сигнала и воспользовавшись обратным преобразованием Фурье
.
Отсюда
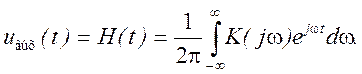
Таким образом, мы попутно получили весьма важный результат - показали, что импульсная характеристика цепи и её комплексный коэффициент передачи связаны между собой преобразованиями Фурье. Эта связь широко используется для определения всех характеристик цепи и анализа их влияния на форму сигналов, передаваемых по цепи. В нашем случае
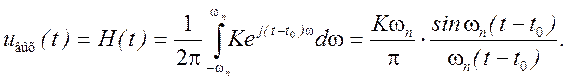
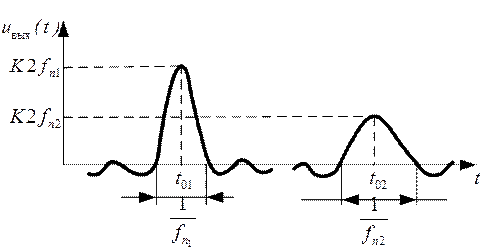
Рис. 3.12
Графики выходных сигналов при различных значениях ωn и t0 показаны на рисунке 3.12. Из анализа
этих графиков следует, что форма входного сигнала при его прохождении через
цепь с ограниченной полосой пропускания существенно исказилась. Эти искажения
проявились в увеличении длительности импульса до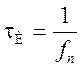 
и
уменьшении амплитуды до величины К2fn.
Причем, чем уже полоса пропускания цепи, тем большими оказываются длительность
выходного сигнала и его фронтов, и тем меньше его амплитуда.
На первый взгляд может показаться, что длительность сигнала может увеличиться настолько, что он будет существовать и при t<0, т.е. реакция цепи наступит раньше, чем поступило на ее вход воздействие. Однако этот вывод неправилен. Действительно, чтобы получить бесконечно большую крутизну АЧХ на частоте ωn, необходимо включить бесконечно большое число звеньев фильтра. А при этом, естественно, время задержки сигнала в фильтре также будет бесконечно большим, чем исключается возможность его появления при t≤0.
Рассмотрим теперь особенности прохождения прямоугольного видеоимпульса через такой фильтр. Так как такой импульс можно представить в виде алгебраической суммы
то и выходной сигнал можно записать в виде суммы
Поэтому, для анализа достаточно найти только одно слагаемое
этой суммы. Воспользуемся для этого предыдущими результатами, заметив, что 
, a цепь является линейной. В силу
указанного, аналогичными соотношениями будут связаны и выходные сигналы цепи,
т.е.
.
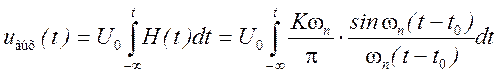Сделаем замену переменных в полученном выражении ωn(t-t0)=x, тогда dx= ωndt, dt= dx/ωn
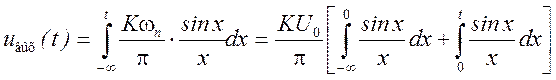
Выражение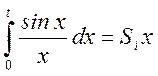 
известно в
математике как интегральный синус, график которого имеет вид (рис. 3.13).
Рис. 3.13
Из анализа этого графика (рис. 3.13) следует, что
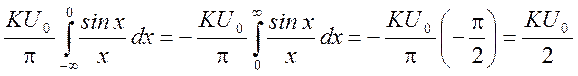
Отсюда
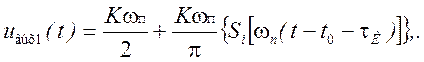
а весь выходной сигнал будет равен
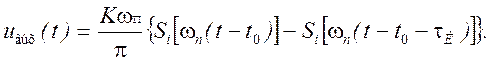
Графики слагаемых сигнала, и всего сигнала в целом, показаны на рисунке 3.14.
Из анализа этих графиков следует, что ограниченность полосы пропускания цепи при ее линейной ФЧХ приводит в основном к увеличению длительности фронтов tФ выходного сигнала до величины
.
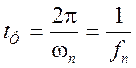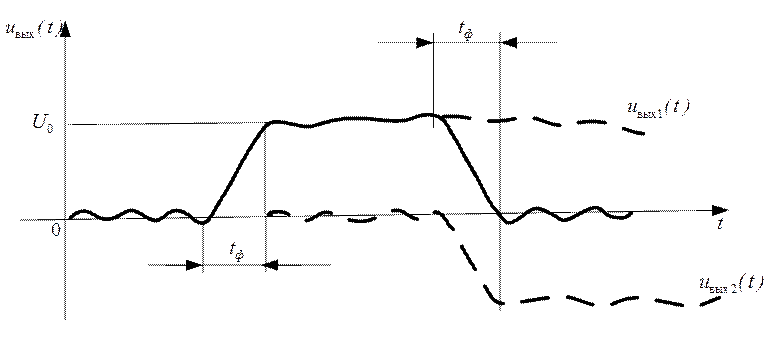
Рис. 3.14
Длительность же сигнала, измеренная на уровне 0,5 от
максимального значения, остается без изменения. Можно считать, что сигнал будет
передаваться по рассматриваемой цепи практически без искажений при условии 
, откуда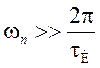 
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.