Таким образом, чем шире полоса пропускания фильтра, тем больше «лепестков» спектра сигнала попадает в эту полосу, а значит тем меньше будет искажаться сигнал в процессе прохождения через фильтр.
К таким же результатам придем и при анализе особенностей прохождения прямоугольных радиоимпульсов через идеальные полосовые фильтры.
И так, влияние ограниченности полосы пропускания цепи на форму выходного сигнала заключается в увеличении длительности его фронта, которая оказывается обратно пропорциональной ширине полосы пропускания цепи.
Пример. Рассчитать изменения фронтов прямоугольного видеоимпульса длительностью τИ≈200мкс и прохождении его через идеальный ФНЧ с полосой пропускания fn=7 кГц.
Решение. Длительность фронта импульса зависит от того,
какая часть спектра входного сигнала проходит через идеальный фильтр. Как
следует из исходных данных, видеоимпульс имеет ширину лепестка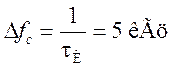 
, а полоса пропускания равна fn = 7 кГц,
следовательно, большая часть спектра сигнала передается без искажений. Фильтр
«отрезает» только высокочастотные составляющие спектра. Это приводит к тому,
что длительность фронта относительно самого сигнала является небольшой. Её
можно рассчитать по формуле
.
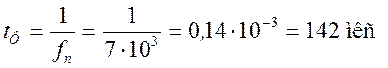Как видно из рисунка 3.15, сигнал несколько «расплылся», но в целом сохранил свою форму.
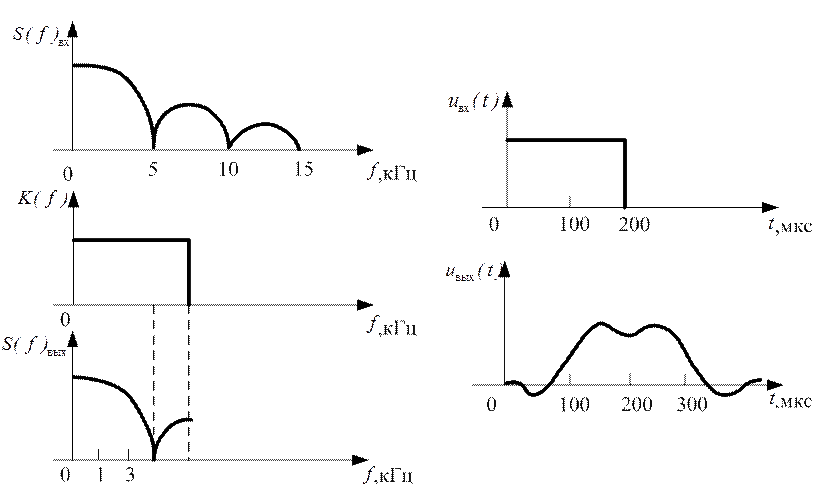
Рис. 3.15
3.5.2. Влияние неравномерности АЧХ цепи на форму передаваемых сигналов
Предыдущие рассуждения относились к идеальным цепям с ограниченной полосой пропускания. Реальные же цепи, как известно, имеют не только ограниченную полосу пропускания, но и неравномерную АЧХ в пределах этой полосы пропускания. Рассмотрим, к каким дополнительным искажениям сигнала это приводит.
Практически у всех цепей АЧХ являются плавными кривыми,
поэтому в пределах полосы пропускания 0+ωnили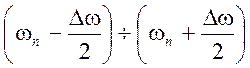 
их можно с достаточной точностью
аппроксимировать суммой
где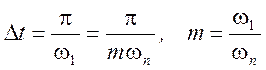 
.
Возможность такой аппроксимации наглядно иллюстрируется на рисунке 3.16.
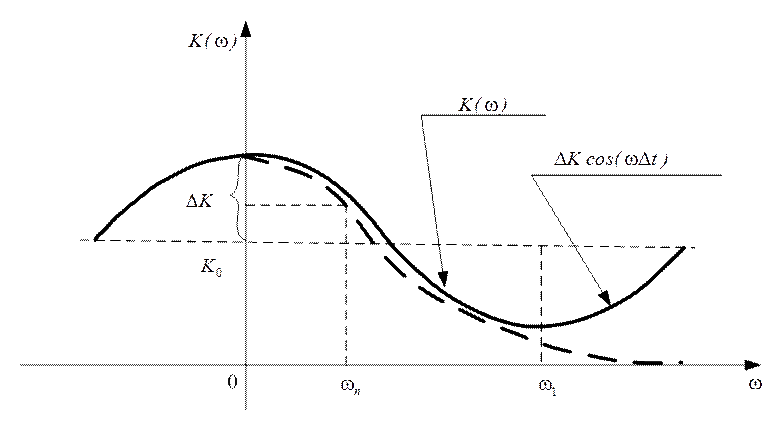
Рис. 3.16
Выбранная нами аппроксимация является очень удобной, так как позволяет для анализа искажений сигнала применить уже известные результаты. Действительно, определяя по общему правилу выходной сигнал цепи с рассматриваемой формой АЧХ (при условии, что АЧХ цепи линейна в пределах полосы пропускания), получим
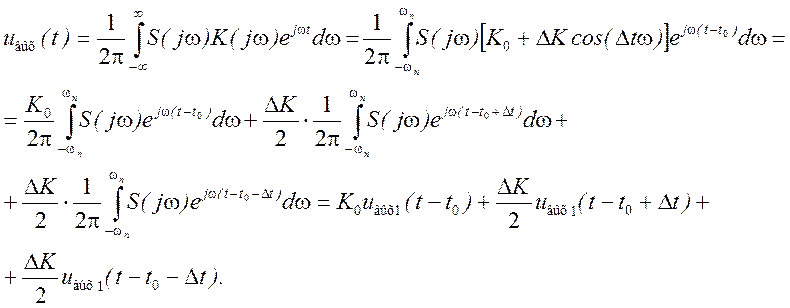
где S(jω) - спектральная плотность входного сигнала, Uвых(t-to)-выходной сигнал цепи с ограниченной полосой пропускания ωn и равномерной в пределах этой полосы АЧХ. Таким образом, выходной сигнал цепи с неравномерной АЧХ можно рассматривать как суперпозицию трех сигналов:
· основного сигнала, задержанного на величину t0 и имеющего искажения, обусловленные ограниченностью полосы пропускания цепи,
·
двух дополнительных сигналов, симметрично расположенных относительно
основного на расстоянии от него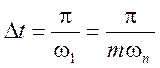 
.
Дополнительные сигналы совпадают по форме с основным, но
меньше его по амплитуде в 
раз и называются
«парным эхом» основного сигнала. Поэтому и сам метод такого анализа называется
методом «парного эхо».
Если АЧХ цепи имеет более сложную форму, то ее можно аппрок-симмировать суммой большего числа тригонометрических функций. Тогда в выходной сигнал будет входить целый ряд «парных эхо».
В качестве примера ниже показаны графики основного и дополнительных слагаемых (вверху) основного сигнала и сам выходной сигнал (внизу) цепи с ограниченной полосой пропускания и нелинейной в пределах этой полосы АЧХ. Графики построены при условии, что на вход цепи поступает прямоугольный видеоимпульс.
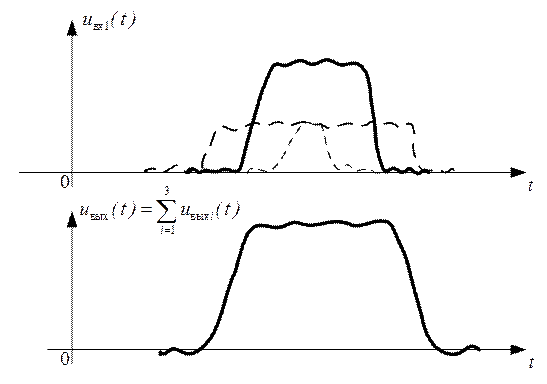Как видно на рисунке 3.17 искажения формы сигналов в реальных
цепях носят более плавный характер, чем в идеальных.
Рис. 3.17
Пример. Проанализировать влияние АЧХ интегрирующей цепи (рис. 3.18) на спектр и форму прямоугольного видеоимпульса.
Решение. Пусть на rC цепь поступает одиночный прямоугольный видеоимпульс длительностью τu и амплитудой U0.
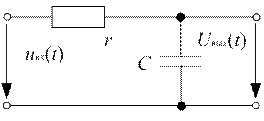
Рис. 3.18
Спектральная плотность входного сигнала определится
,
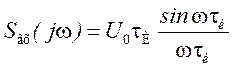комплексная частотная характеристика цепи по напряжению иметь в виду
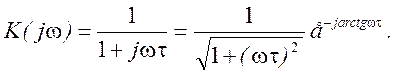
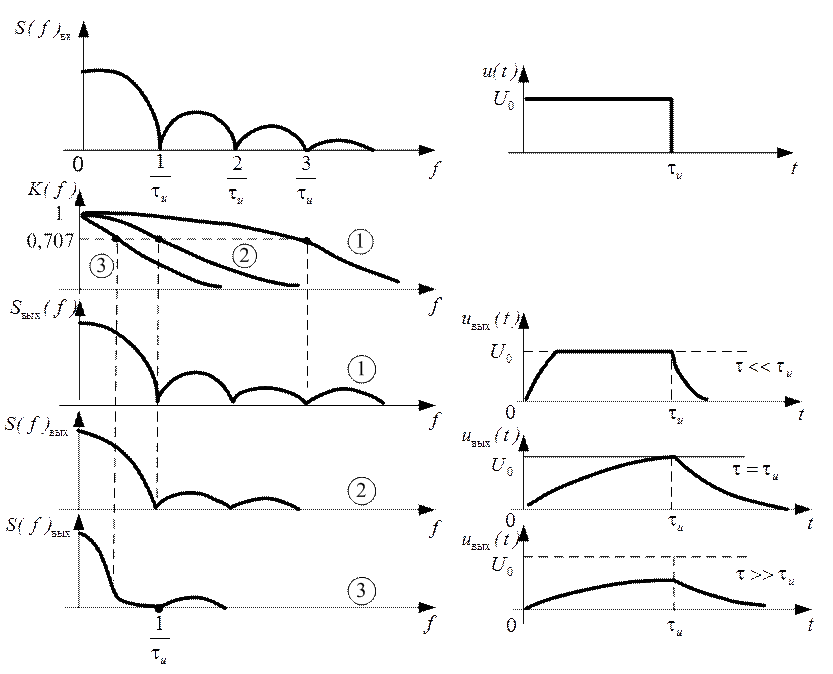
Рис. 3.19
Спектральная плотность выходного сигнала определится
.
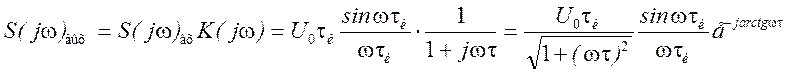Сигнал на выходе цепи
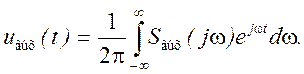
Здесь можно выделить три случая.
· Постоянная времени цепи τ меньше длительности импульса τu. В этом случае спектр сигнала пройдет через цепь почти без искажений.
· Постоянная времени τ равна длительности импульса (τ=τu) тогда амплитуда импульса нарастет до 0,63 своего максимального значения как раз за время τu, после чего она будет по экспоненте убывать. В данном случае спектр сигнала теряет часть высокочастотных составляющих, что приводит к значительным фронтам.
· В случае, когда постоянная времени цепи больше длительности импульса (τ>τu), сигнал теряет большую часть своих спектральных составляющих, что приводит к значительному увеличению фронтов импульсов.
4. ОПЕРАТОРНЫЙ МЕТОД АНАЛИЗА ПРОЦЕССОВ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
4.1. Основные определения и теоремы операционного исчисления
4.1.1. Общие сведения об операторном методе анализа цепей и его свойствах
При анализе процессов, протекающих в линейных электрических цепях, возникает необходимость решения линейных дифференциальных и интегро-дифференциальных уравнений. Такие уравнения просто решаются только при нулевых начальных условиях, поэтому в теории электрорадиоцепей нашел широкое применение так называемый операторный метод, в основе которого лежит преобразование Лапласа.
Сущность операторного метода заключается в том, что исходной функции u(t) вещественного переменного (в нашем случае времени t), называемой оригиналом, ставится в соответствие функция U(p) комплексного переменного p=σ+jω , называемая изображением
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.