Электротехника \ Радиотехнические цепи и сигналы

Нестационарные процессы в электрических цепях, страница 2

Рассмотрены типовые сигналы, применяемые в радиотехнике и их аналитическое и графическое представление во временной области. Показана взаимосвязь одиночных, периодических и пачечных сигналов, показана взаимосвязь видеосигналов и радиосигналов.

Сигналы в спектральной области

Аналитическое или графическое представление сигналов как функции частоты является представлением сигналов в спектральной (частотной) области.

Различают представление сигналов в спектральной области с дискретным и сплошным спектрами.

Можно доказать, что периодические сигналы обладают дискретными спектрами, а одиночные и пачечные сигналы – сплошными.

Пусть некоторый периодический сигнал представлен совокупностью u(t) гармонических колебаний    .

Совокупность частот  представленных колебания является частотным спектром данного сигнала.

Совокупность амплитуд на соответствующих частотах

             ...     

   ...

является амплитудно-частотным спектром данного сигнала.

Совокупность начальных фаз на соответствующих частотах

          .. 

     ...

является фазо-частотным спектром данного сигнала.

Амплитудно-частотный спектр (АЧС) (рис. 1.19) и фазо-частотный спектр (ФЧС) (рис. 1.20) могут быть изображены в виде системы, состоящей из двух графиков.

Рис. 1.20

Для одиночных и пачечных сигналов АЧС и ФЧС будут сплошными.

Для расчета спектров, т.е. для представления сигналов как функции частоты, используют следующие основные приемы:

- тригонометрические преобразования,

- интегральное преобразование Фурье,

- разложение в ряд Фурье.

В результате интегрального преобразования Фурье вычисляют спектральную плотность заданного одиночного сигнала и представляют ее в показательной форме записи

,

здесь  - спектральная плотность;

   - модуль спектральной плотности;

  - аргумент спектральной плотности;

   - сигнал.

Аналитические выражения  или , а так же  или  являются зависимости, описывающими АЧС и ФЧС данного сигнала.

В результате разложения в ряд Фурье представляют заданный периодический сигнал в виде совокупности гармонических составляющих:

,

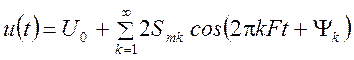где 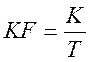   - частота гармонической составляющей с номером ;

         - постоянная составляющая;

         - амплитуда гармонической составляющей с номером K;

         - начальная фаза гармонической составляющей с номером .

Расчет  и  проводится согласно выражения

,

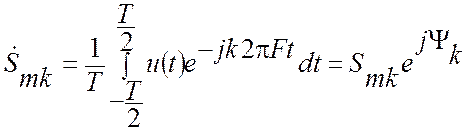где - комплексная амплитуда ряда Фурье.

________________Расчет  проводится аналогично, при :

Между спектральной плотностью  и комплексной амплитудой ряда Фурье существует связь:

,

                  

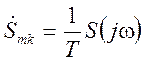которая позволяет, зная значения спектральной плотности, вычислить комплексную амплитуду ряда Фурье путем вычисления спектральной плотности на частотах  и умножения полученных значений на множитель .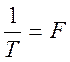

Свойства преобразований Фурье

При спектральном анализе сигналов объем математических преобразований в ряде случаев можно существенно сократить, если использовать следующие свойства преобразований Фурье.

·  Свойство аддитивности

Если ≓, ≓, ≓, ..., ≓, то для ≓.

·  Свойство однородности

Если ≓, то для ≓, где  - постоянный множитель.

·  Свойство сдвига аргумента

Если ≓, то

          ≓

·  Свойство смещения

Если ≓, то

         ≓

·  Свойство дифференцирования

Если ≓, то

         ≓

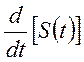·  Свойство интегрирования

Если ≓, то

         ≓

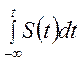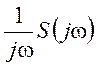
Ширина спектра сигналов

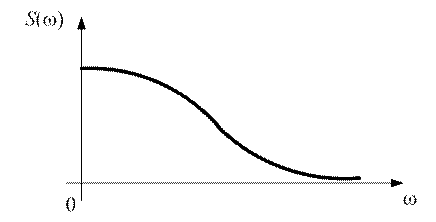
Рис.1.21

На рисунке 1.21 приведен график амплитудно-частотного спектра произвольно выбранного некого одиночного сигнала, причем модуль спектральной плотности монотонно убывает с      ростом значения частоты.

Для большинства одиночных сигналов характерно такое распределение модуля спектральной плотности от частоты.

Вычислив интегралы

,

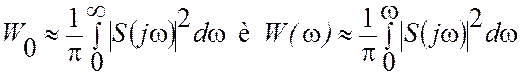получим значения, пропорциональные соответственно полной энергии сигнала W0, и энергии сигнала W(ω), сосредоточенной в полосе частот от 0 до .

Отношение

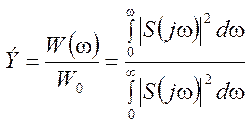
показывает, какая часть всей энергии сигнала сосредоточена в диапазоне частот от 0 до .

Шириной спектра сигнала со сплошным спектром называют область частот (от 0 до  или от  до  ), в пределах которой

заключена основная часть (принята величина 90 %) энергии сигнала.

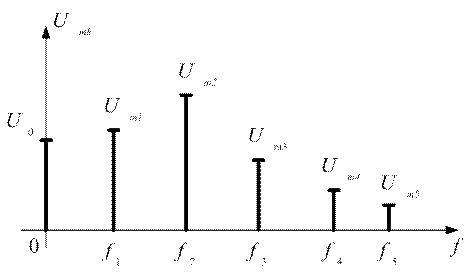
Рис.1.22

На рисунке 1.22 показан амплитудно-частотный спектр некого периодического сигнала, причем амплитуды спектральных составляющих монотонно или немонотонно убывают с ростом частоты.

Энергия сигналов, обладающих дискретным спектром, пропорциональна:

,

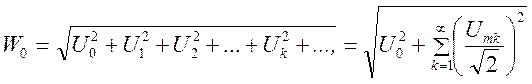где - постоянная составляющая;

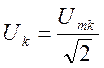      - действующее значение -й составляющей.

Если вычислить

,

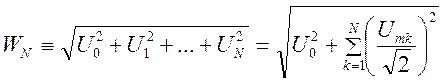получим значение, пропорциональное энергии сигнала в полосе частот от 0 до некоторой частоты .

Отношение

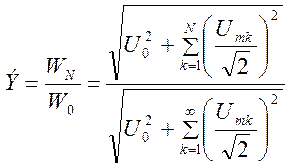
показывает, какая часть энергии сигнала с дискретным спектром сосредоточена в диапазоне частот от 0 до .

Шириной спектра сигналов с дискретным спектром называют область частот (от 0 до   или от  до  ), в пределах которой заключена основная часть (не менее 90%) энергии сигнала.

Сравнивая определения ширины спектра сигналов со сплошным спектром и с дискретным спектром, можно заметить отличие ("90% и не менее 90%"), обусловленное дискретным характером изменения величины .

Спектры видеосигналов сосредоточены в области низких частот, радиосигналов – в области частот несущего колебания.

Важнейшей характеристикой сигналов в радиотехнике является база сигнала (коэффициент широкополостности), равная произведению длительности сигнала (τс) на ширину его спектра(Δƒс) n=τcΔfc.

Сигналы, у которых база сигнала порядка 1, называют простыми (узкополосными) сигналами. К простым сигналам относят одиночные и периодические последовательности импульсов без внутриимпульсной модуляции.

У сложных (широкополосных) сигналов n»1. сложными сигналами являются радиосигналы с внутриимпульсной частотной или фазо – кодовой модуляцией, а также, пачки видео и радиоимпульсов.

1.2. ОДИНОЧНЫЕ СИГНАЛЫ И ИХ СПЕКТРЫ

1.2.1. Одиночные видеосигналы и их спектры

Рассмотрим спектры некоторых простейших видеосигналов.

Спектр дельта-функции

 Дельта-функцией называется сигнал вида (рис. 1.23): 

Скачать файл