Выходной сигнал имеет следующие особенности:
· амплитуда выходного сигнала изменяется по закону изменения АЧХ цепи, через которую этот сигнал прошел;
· частота выходного сигнала изменяется аналогично закону изменения частоты входного сигнала;
· таким образом, сигнал на выходе имеет не только угловую (частотную), но и амплитудную модуляцию.
Рассмотрев данный вопрос, мы провели анализ принципа работы автоматического измерителя амплитудно-частотных характеристик, нашли широкое применение в радиотехнике и применяются при настройке радиоэлектронной аппаратуры.
3.4. Особенности передачи сигналов со сплошными спектрами через линейные электрические цепи
3.4.1. Общие сведения о неискажающей цепи
Как показано ранее, форма электрических сигналов, проходящих через цепи с избирательными свойствами по частоте, изменяется. В ряде случаев такие изменения являются нежелательными, так как они искажают форму входных сигналов, что приводит, к потере части закодированной в этих сигналах информации. Выясним, какими же частотными характеристиками должны обладать неискажающие цепи, т.е. цепи, не изменяющие форму передаваемых по ним сигналов. Полагаем при этом, что искажениями не являются задержка сигналов на время t0, изменение его амплитуды в к раз, а в случае радиосигналов - и изменение его начальной фазы на величину φ0. Поэтому, если входным сигналом неискажающей цепи является сигнал
то ее выходной сигнал в общем случае можно записать как
.
Отсюда следует, что комплексный коэффициент передачи неискажающей цепи имеет вид
.
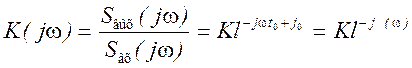Графики модуля (АЧХ) и аргумента (ФЧХ) такого комплексного коэффициента показаны на рисунке 3.7 (слева). Чтобы цепь была неискажающей и для видеосигналов, необходимо в выражении принять φ0=0, тогда график φ(ω) пройдет через начало координат.
Цепи с комплексным коэффициентом передачи являются неискажающим для любых сигналов со сколь угодно широкими спектрами. Однако спектры реальных сигналов сосредоточены в сравнительно узком диапазоне частот. Поэтому для них неискажающими можно считать и цепи, имеющие равномерный модуль (K(jω)) и линейно изменяющейся по частоте аргумент φ(ω) комплексного коэффициента передачи только в полосе частот, занимаемых спектром сигнала. Реализация таких неискажающих цепей оказывается гораздо проще, чем идеальных.
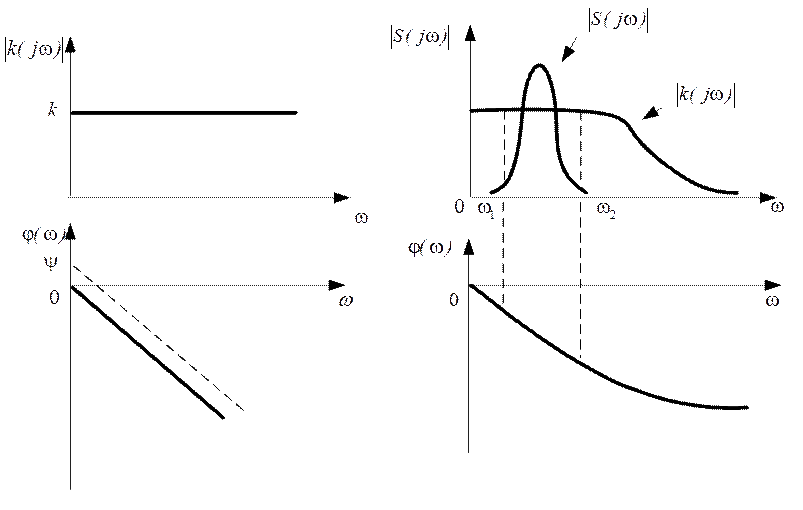
Рис. 3.7
Неискажающие цепи являются, по сути устройствами, предназначенными для задержки сигналов (линиями задержки). Примером идеальной линии задержки является свободное пространство (эфир), которое способно задерживать сигналы на самое различное время. Так, излучаемые в пространство зондирующие импульсы радиолокационных станций задерживаются в нем в процессе распространения от РЛС до цели и обратно на время от нескольких микросекунд до десятков миллисекунд. Интервал же времени между моментами излучения сигналов передающими устройствами советских космических кораблей «Венера» и момента их приема на Земле составляет около 5 минут.
Необходимо задержать сигналы на определенное время в технике возникает очень часто. Для этих целей возможно использование различных цепей с накопительными элементами. Для их характеристики вводят понятия фазового и группового времен задержки.
Фазовое время задержки tф определяется запаздыванием одной синусоидальной составляющей спектра сигнала при прохождении ее через цепь и математически вводится как
.
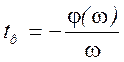Так, для неискажающей цепи с φ0=0 tф=t0. Если же аргумент комплексного коэффициента передачи цепи нелинеен или линеен, но не проходит через начало координат (т.е. φ0≠0), то фазовое время задержки не равно запаздыванию сигналов в цепи.
В таких случаях используют время групповой задержки tгр; которое определяет запаздывание в цепи сигналов, имеющих очень узкий спектр (т.е. «группу» спектральных составляющих).
Математически это время вводится как
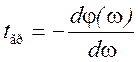
В частности, для идеальной неискажающей линии задержки tгр=t0 при любом значении φ0. Если же цепь имеет нелинейную зависимость φ(ω), то различные участки спектра сигнала (т.е. «группы» спектральных составляющих) имеют различное время группового и фазового запаздывания, не равное в общем случае задержки сигналов t0. В результате форма выходного сигнала будет изменяться даже в том случае, если (К(jω) цели будут равномерным на всех частотах. Для всех сигналов, кроме сигналов с линейной частотной модуляцией, эти изменения заключаются в увеличении длительности и искажении («расплывании») огибающей, как показано на рисунке 3.8
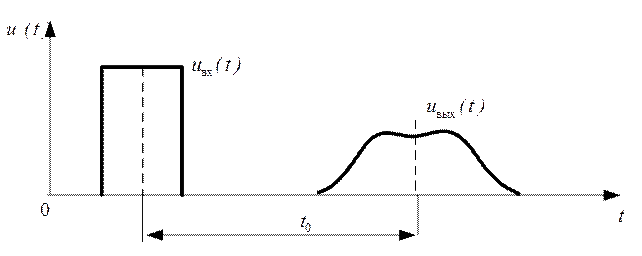
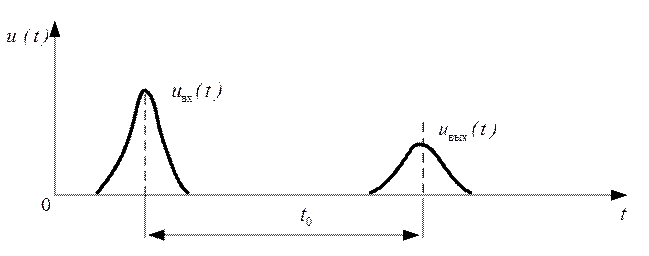
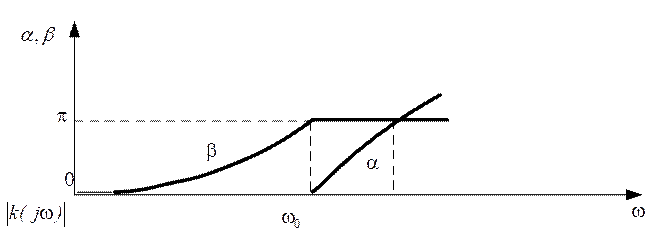
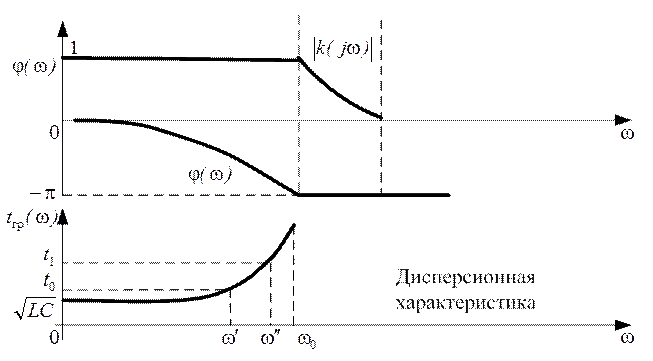
Рис. 3.8
В случае же сигналов с линейной частотной модуляцией при определенных условиях может наблюдаться не растяжение, а сжатие выходного сигнала во времени.
3.4.2. Использование линейных цепей для задержки сигналов
Рассмотрим в качестве примеров возможности последовательного колебательного контура и фильтра нижних частот для задержки сигналов. Комплексный коэффициент передачи последовательного контура, можно представить, как известно, в виде
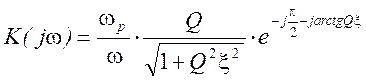
Для частот, близких к резонансной частоте контура, это выражение легко преобразуется в более простое:
,
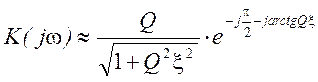здесь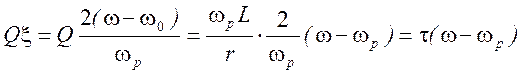 
,
где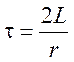 
- постоянная времени контура.
Отсюда
.
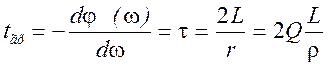Таким образом групповое время задержки сигналов в контуре оказывается равным его постоянной времени. Включая по каскадной схеме К таких контуров, можно увеличить групповое время задержки до величины Кτ.Но так как для выполнения условия
справедливого для полосы частот занимаемой спектром сигнала, добротности контуров следует выбирать небольшими, то и задержка сигналов в такой системе контуров оказывается сравнительно маленькой - от нескольких микросекунд до нескольких десятков микросекунд.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.