Нестационарные процессы в электрических цепях, страница 13

затем выполняют построение графиков, после чего можно составить аналитическое выражение переходного процесса.

 ПРИМЕР 1. Провести анализ процессов в схеме (рис. 2.39), изображенной на рисунке.

Начальные условия:

конденсатор С заряжен до напряжения Е₁.

Принужденная составляющая:

после коммутации напряжение на конденсаторе постепенно уменьшится и станет равным Е₂.

График напряжения приведен на рисунке и имеет выпуклость в сторону принужденной составляющей.

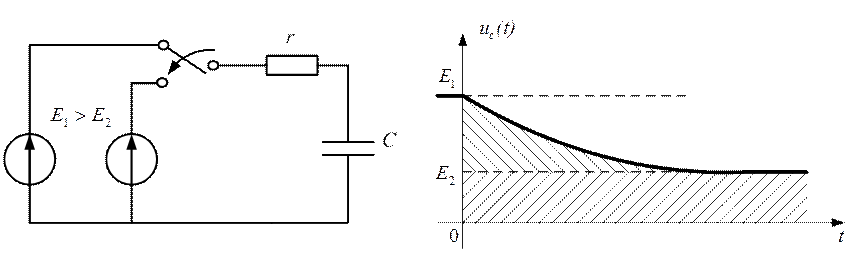
Рис.2.39

Аналитическое выражение u_c(t) можно записать:

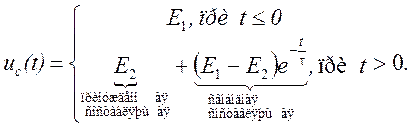
ПРИМЕР 2. Рассмотрим переходные процессы в схеме (рис.2.40), у которой отличие от предыдущей состоит в том, что полярность источника Е₂противоположна.

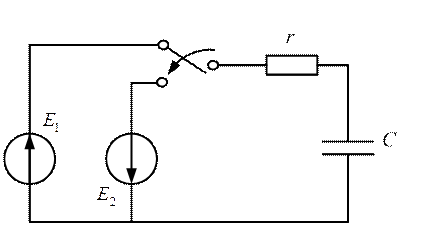
Рис.2.40

Начальные условия: u_c(0)=E₁

Принужденная составляющая:

График процесса u_c(t) приведен на рисунке  2.41, конденсатор С будет перезаряжаться  от напряжения Е₁ до –Е₂.

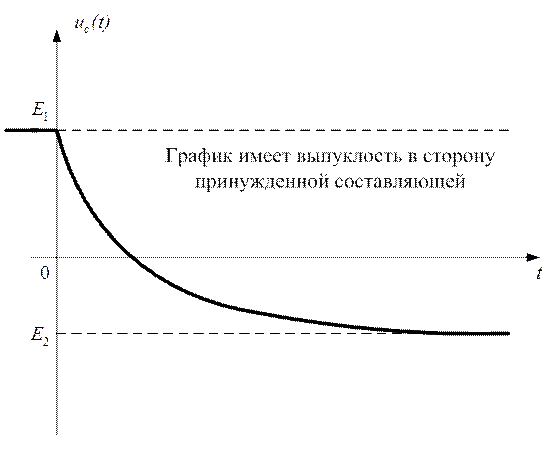
Рис. 2.41

Аналитическое выражение u_c(t) можно записать следующим образом:

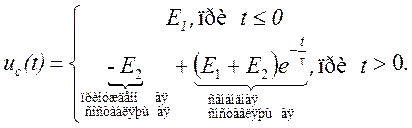
Аналитическое выражение в обоих случаях составить довольно просто: необходимо к значению принужденной составляющей прибавить экспоненту (убывающую или нарастающую), начальное значение которой равно разности между начальным значением и принужденной составляющей.

ПРИМЕР 3.

Начальные условия: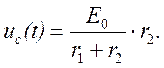  

Принужденная составляющая: .

Конденсатор был заряжен до напряжения 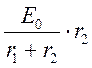, после размыкания ключа он дозарядится до Е₀.

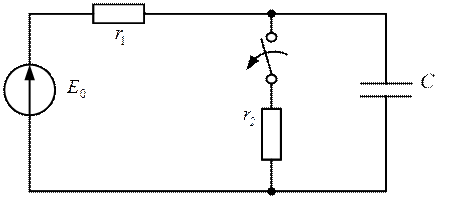
Рис.2.42

График, приведенный на рис. 2.43, имеет выпуклость в сторону принужденной составляющей.

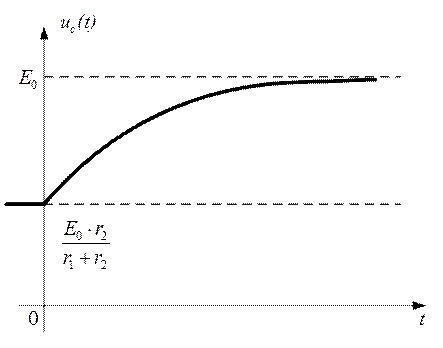
Рис. 2.43

Аналитическое выражение u_c(t) имеет вид:

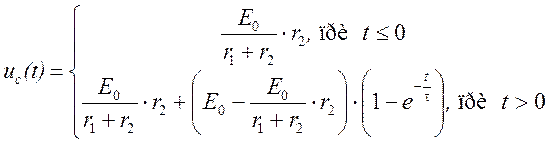
или

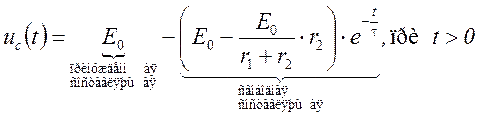
б) для цепей второго порядка:

Анализ процессов в цепях второго порядка отличается тем, что необходимо установить характер процессов (колебательный или апериодический).

ПРИМЕР 4. Пусть параметры r, L, С (рис. 2.44) таковы, что Q>>0,5. Это значит, что процесс будет носить колебательный характер().

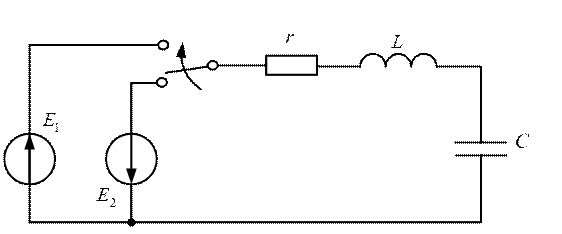
Рис. 2.44

Начальные условия:

Принужденная составляющая: Е₁

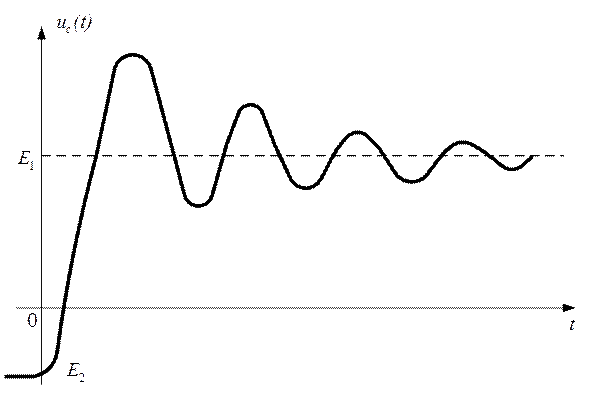
Рис. 2.45

График колебательного перезаряда емкости имеет вид, изображенный на рисунке 2.45.

Аналитическое выражение u_c(t), будет:

 .

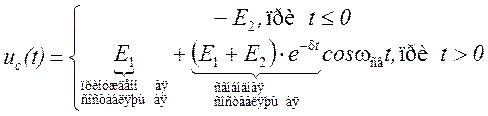Вывод: Качественный анализ переходных процессов можно осуществлять, не решая дифференциального уравнения цепи.

2.9. Метод наложения

2.9.1. Общие сведения о методе наложений

Применяя рассмотренный ранее классический метод, мы провели анализ переходных процессов при подключении цепей к источникам постоянной или синусоидальной ЭДС, а также свободных процессов в цепях.

Исследование переходных процессов при подключении источников ЭДС произвольной формы наталкивается на ряд математических трудностей, связанных с расчетом принужденной составляющей.

Существует метод, позволяющий непосредственно проводить анализ переходных процессов при подключении цепей к источникам ЭДС произвольной формы или рассчитывать сигнал на выходе заданной цепи при подаче на вход цепи сигнала произвольной формы.

Сущность метода состоит в следующем. Обычно, при решении какой-либо сложной задачи удается выделить наиболее простой случай, для которого решение получается достаточно просто, но общей силы не имеет. Объединяя  путем наложения частные случаи, можно получить полное решение, пригодное в общем случае.

Допустим, что внешнее произвольное воздействие х(t) можно представить совокупностью более простых, аналитически однотипных функций х_к(t), т.е.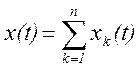

Допустим, что для данной цепи для каждой функции х_к(t) найдена реакция y_k(t). Тогда, на основании принципа суперпозиции можно утверждать, что реакция цепи и у(t) на воздействие x(t) равна сумме реакций y_k(t) т.к. .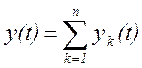

Таким образом, полное решение задачи может быть разложено на 2 этапа: первый - определение реакции у_к(t) на заданное простое воздействие x_k(t),второй - суммирование (наложение) частных решений y_k(t).

В качестве элементарных воздействий применяют обычно следующие два типовых импульсных сигнала.

2.9.2. Типовые импульсные воздействия и их свойства

А. ЕДИНИЧНАЯ СТУПЕНЧАТАЯ ФУНКЦИЯ 1(t) 

(функция Хевисайда, функция включения)

Функция 1(t) имеет следующие значения: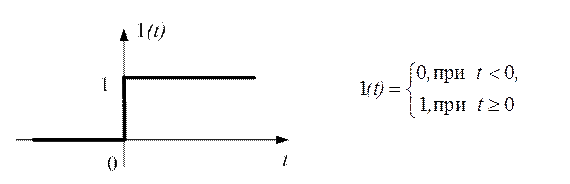

Рис. 2.46

При смещении такой функции по оси абсцисс вправо на время(запаздывание на время ), ее можно выразить в виде:

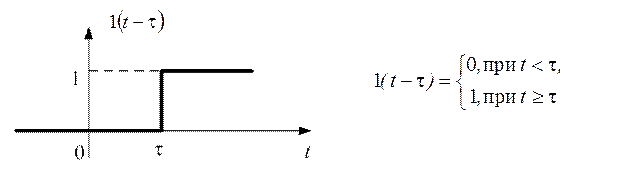
Рис. 2.47

Использование таких ступенчатых сигналов в теории цепей не случайно. Например, включение постоянного напряжения на вход устройства при помощи ключа может быть представлено при помощи этих функций.

Б. ДЕЛЬТА-ФУНКЦИЯ  (функция Дирака).

Для дельта-функции справедливы соотношения:

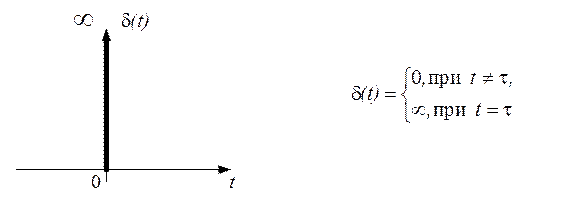
Рис. 2.48

При смещении дельта-функции вправо по оси абсцисс на время(запаздывание на время ), справедливы следующие соотношения:

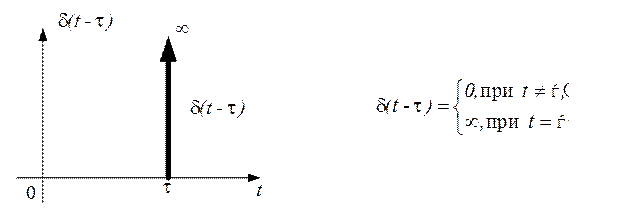
Рис. 2.49

В практическом отношении ценность - функции заключается в возможности использования ее свойств:

Свойство фильтрации, дающее возможность выделить(отфильтровать) значение произвольной функции f(t) в данный момент времени.

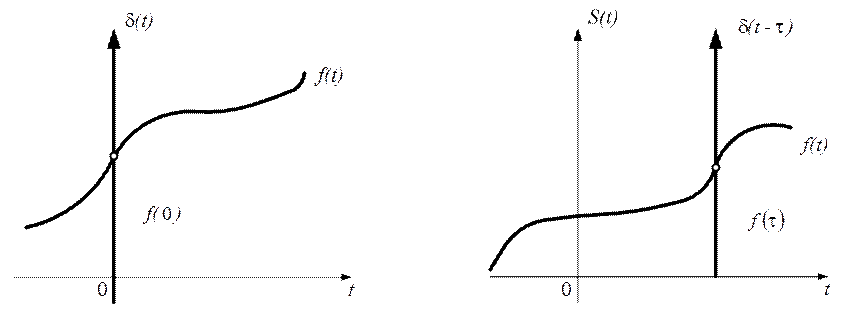
         а) 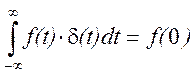                                     б)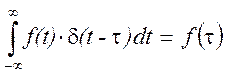           

Рис. 2.50

На рисунке 2.50 а) (слева) показано выделение значения функции f(t) в нулевой момент времени.

На рисунке 2.50 б) (справа) показано выделение значения этой же функции в произвольный момент времени .

Свойство, устанавливающее связь между - функцией и функцией включения 1(t)

     

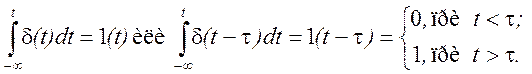
С другой стороны

,

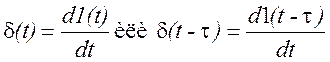т.е. - функция равна производной единичной ступенчатой функции.

Импульсные воздействия близкие к - функции, встречаются на практике в виде коротких импульсов.

2.9.3. Временные характеристики электрических цепей, связь между ними

Временными характеристиками цепи является переходная и импульсная характеристики, являющиеся функциями времени, определяющие реакцию цепи на заданное типовое воздействие.

Переходной характеристикой G(t) называют реакцию цепи на воздействие ступенчатой функции 1(t) при нулевых начальных условиях цепи.

          Импульсной характеристикой H(t) называют реакцию цепи на воздействие - функции при нулевых начальных условиях

 Рис. 2.51

Между сигналами на входе и на выходе линейной электрической цепи (рис. 2.51) есть связь, выражаемая следующими соотношениями: