Нестационарные процессы в электрических цепях, страница 22

Решить полученную систему алгебраических уравнений относительно изображения искомой величины.

Перейти от изображения искомой величины к ее оригиналу.

Такой алгоритм можно использовать для расчетов процессов в любых цепях при любых начальных условиях. Однако процедуру расчетов можно во многих случаях значительно упростить, если перейти от обычной схемы к её эквивалентной операторной схеме. Действительно, в результате перехода от

оригинала к изображению каждому элементу цепи можно поставить в соответствие его операторный эквивалент:

для сопротивления r (рис. 4.2): i(t)÷I(p); u_r(t)÷U(p)=rI(p)

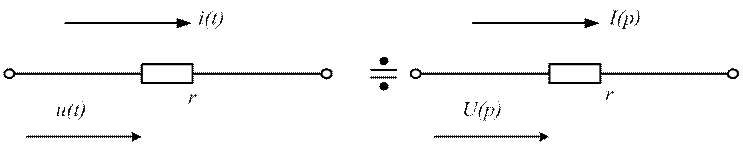
                        Рис. 4.2

для индуктивности L (рис. 4.3): i(t)÷I(p); u_L(t)÷U_L(p)

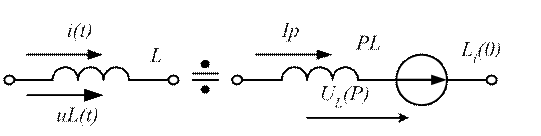
           Рис. 4.3

для емкости С (рис. 4.4):

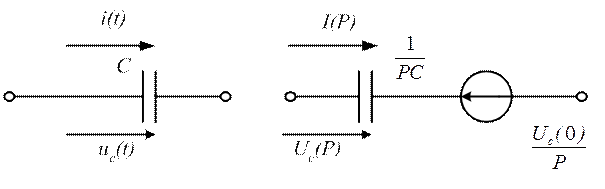
    Рис. 4.4

Используя, эквиваленты элементов электрических цепей, последовательному контуру можно поставить в соответствие эквивалентную операторную схему, приведенную на рисунке 4.5. Она получена из исходной схемы заменой индуктивности L и емкости С операторными сопротивлениями pL и 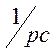 с учетом ненулевых начальных условий в виде дополнительных источников ЭДС  L_i(0), совпадающего с направлением тока, и 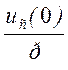направленного против тока, протекающего в цепи.

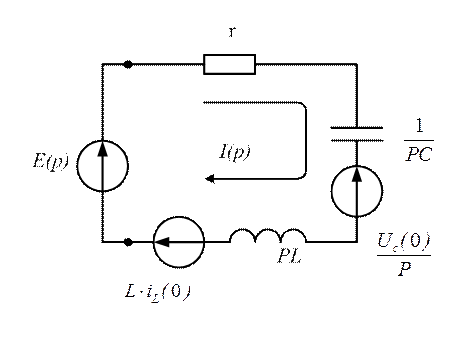
Рис. 4.5

Для эквивалентных операторных схем выражения законов Ома и Кирхгофа в операторной форме совпадают с выражениями этих законов в комплексной форме.

Следует отметить, что переход к эквивалентной операторной схеме, особенно при нулевых начальных условиях, можно произвести мысленно, т.е. определять необходимые изображения токов или напряжений можно и по исходной схеме цепи, считая, что сопротивления элементов L и С равны Z_L(р)=pL и 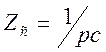, включив при ненулевых начальных условиях последовательно с L и С дополнительные источники ЭДС L_i(0) и u_c(0)/р.

Обобщая проделанные выкладки, можно предложить следующий алгоритм расчета переходных процессов в цепи с помощью ее эквивалентной операторной схемы:

·  Определить начальные условия u_c(0) и Li(0).

·  Составить эквивалентную операторную схему с учетом начальных условий.

·  Выбрать оптимальный метод решения и определить изображение выходного сигнала.

·  Перейти от изображения сигнала к его оригиналу.

4.2. Применение операторных методов для анализа переходных процессов в цепях

4.2.1. Расчет цепей с помощью эквивалентных операторных схем

Рассчитаем переходные процессы в электрических цепях с помощью эквивалентных операторных схем на конкретных примерах.

Пример 1. Найти выражение для мгновенного значения тока в цепи rL (рис. 4.6) при отключении её от источника постоянного напряжения Е.

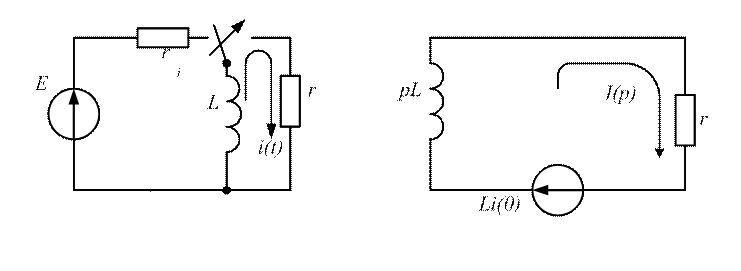
Рис. 4.6

            1. В соответствие с алгоритмом определим начальные условия Li(0).

До коммутации индуктивность L была подключена к источнику ЭДС через сопротивление r_i. Следовательно по ней протекал ток I₀ величина которого равна

.

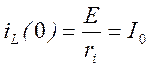2. Эквивалентная операторная схема строится для момента времени прошедшего после коммутации и имеет вид, приведенный на рисунке справа. Начальные условия учитываются наличием в цепи источника ЭДС Li(0).

3. Для определения изображения тока I(p) воспользуемся законом Ома в операторной форме:

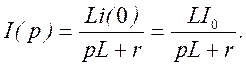
4. Остается перейти от изображения I(p) к оригиналу i(t). В этих целях воспользуемся таблицей операторных соответствий, из которой находим:

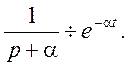
Приведем изображение тока к табличному виду, разделив числитель и знаменатель на величину L:

                                 

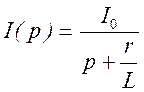
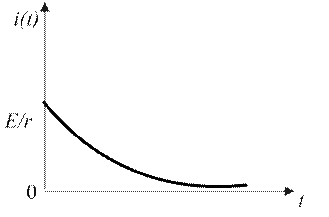
Рис.4.7

Следовательно, мгновенное значение тока в цепи будет определяться выражением

,

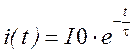где

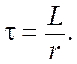
График переходного процесса, описываемый полученным соотношением, приведен на рисунке 4.7

Пример 2. Найти закон изменения напряжения на емкости в последовательном колебательном контуре, к которому в момент времени t=0 подключается источник ЭДС e(t).

1. Из анализа схемы (рис. 4.8 а) (слева)) и условия задачи следует, что в начальный момент времени ток в цепи отсутствует, напряжения на емкости нет, т.е.

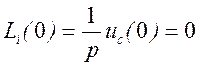
               а)                                                                   б)

Рис. 4.8

2. Эквивалентная операторная схема цепи принимает вид, приведенный на рисунке 4.8(справа).

3. Изображение напряжения на емкости U_c(p) можно рассчитать с помощью закона Ома в операторной форме:

.

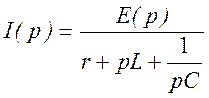Следовательно

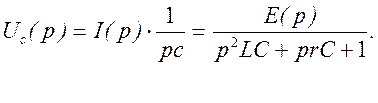
Определим корни знаменателя, для чего приравняем его нулю

.

Отсюда

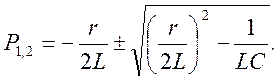
Введем обозначения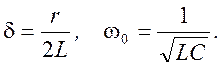

Тогда                          

Выражение для изображения напряжения на емкости примет вид

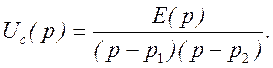
Используя полученное выражение, можно определить закон изменения напряжения на емкости при различных видах подключаемой Э.Д.С.

Пусть e(t)=δ(t), тогда Е(р)=1. Следовательно

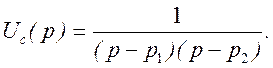
Применим к полученному соотношению обратное преобразование Лапласа, используя таблицу соответствий

.

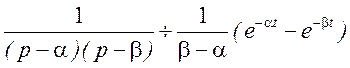Тогда напряжение на емкости определится соотношением

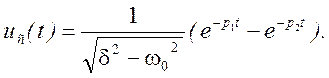
Как известно, в зависимости от соотношения между корнями знаменателя изображения U_c(p) возможны два вида переходного процесса:

·  апериодический, если корни вещественные . График переходного процесса приведен на рисунке 4.9.

·  колебательный, если корни комплексно-сопряженные . Добротность контура будет высокой. График переходного процесса на нижней части рисунка 4.9. Полученные результаты совпадают с известными ранее, но процесс их получения значительно проще.

Рис. 4.9

4.2.2. Операторные передаточные функции электрических цепей

Операторной передаточной функцией линейной электрической цепи К(р) (рис. 4.10) называется отношение изображения выходной электрической величины U₂(p) к изображению входной величины U₁(p) при нулевых начальных условиях: