Нестационарные процессы в электрических цепях, страница 15

В приведенном выражении  - максимальная частота, на ко­торой спектральная плотность описываемого сигнала отлична от нуля. Выбираемый интервал дискретизации  и частота  связаны соотношением 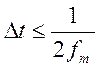. Это значит, что соседние функции вида 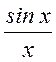 должны отстоять друг от друга на интервал времени не больше, чем .

На рисунке, приведенном ниже, показана графическая интерпретация представления произвольного сигнала при помощи функции вида .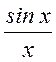

·  Б. Применение функций вида  или .

Большой класс электрических сигналов может быть представлен в виде разложения в ряд:

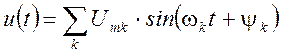 или

,

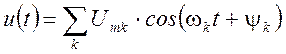где  - амплитуда k-й синусоиды;

 - частота k-й синусоиды;

 - начальная фаза k-й синусоиды.

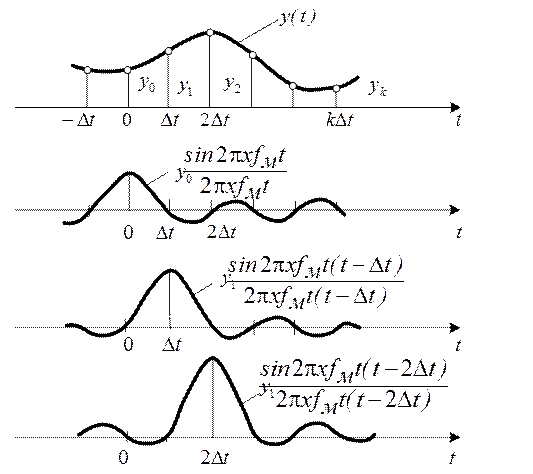
Рис. 2.58

·  В. Применение дискретных сигналов.

Необходимость рассмотрения дискретных сигналов возникла в связи с развитием цифровых методов обработки сигналов на ЭВМ.

Первоначально в радиотехнике использовались исключительно сигналы аналогового типа (непрерывные сигналы). В настоящее время в ряде случаев на смену аналоговым приходят дискретные сигналы.

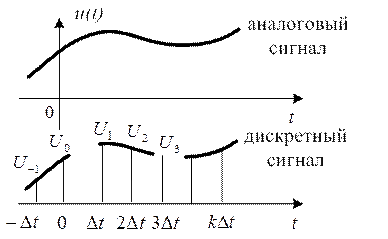
 На рисунке 2.59 показана связь и различие между аналоговым сигналом и дискретным сигналом, которым заменяют данный аналоговый сигнал.

Рис. 2.59

Нетрудно представить себе техническое устройство, которое осуществляет операцию дискретизации аналогового сигнала (рис. 2.60).

Рис. 2.60

Основное свойство дискретного сигнала состоит в том, что его значения определены не для всех моментов времени, а лишь в счетном множестве точек (…t_-1, t₀, t₁, t₂…).

Математически дискретный сигнал может быть выражен следующим образом

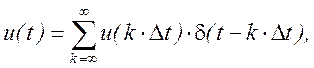
здесь   т.д.

При необходимости может быть осуществлено восстановление непрерывного сигнала по данному дискретному сигналу.

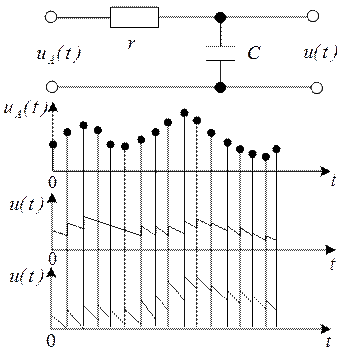Для восстановления можно применить например rс-цепь. На рисунке 2.61 показано, как влияет постоянная времени цепи τ=r*с на качество восстановления непрерывного сигнала по данному дискретному сигналу. Однако в любом случае имеют место некоторые искажения исходного сигнала.

Рис. 2.61

2.9.7. Принцип цифровой обработки сигналов

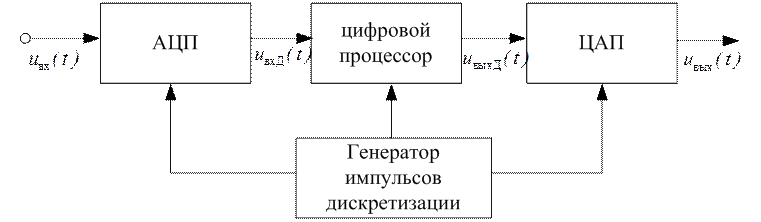
Рис. 2.62

На рисунке приведена структурная схема для цифровой обработки сигналов. Непрерывный входной сигнал u_вх(t) поступает в аналого-цифровой преобразователь (АЦП), который преобразует его в дискретный u_вхд(t). Полученный дискретный сигнал поступает в цифровой процессор ЭВМ, в памяти которой может храниться некоторое число предшествующих значений (отсчетов) входного и выходного сигналов. На основе имеющейся в ЭВМ информации о сигнале и заданной программы осуществляется вычисление значений выходного сигнала u_выхд(t),которые при необходимости могут быть преобразованы в непрерывный сигнал u_вых(t) при помощи ЦАП (цифро-аналового преобразователя).

Преимуществом такого способа обработки на ЭВМ является то, что значения выходного сигнала могут быть вычислены значительно быстрее, чем имели бы место изменения сигнала в реальной цепи. Это позволяет при помощи одной ЭВМ осуществлять обработку многих аналоговых сигналов по различным программам.

Реализация программ цифровой обработки сигналов может быть основана на применении дискретной формы интеграла Дюамеля.

Ранее было рассмотрено понятие импульсной характеристики цепи. Введем понятие импульсной характеристики цифрового фильтра (ЭВМ с заложенной в ней программой для обработки дискретных сигналов называют цифровым фильтром). По аналогии с понятием импульсной характеристики цепи импульсная характеристика цифрового фильтра представляет собой дискретный сигнал , который является реакцией на δ(t)-функцию в цифровой форме.

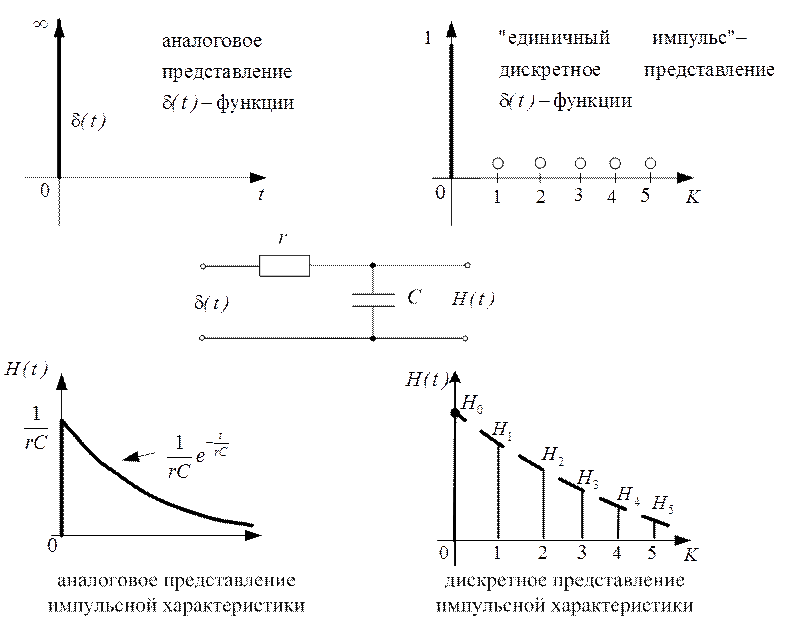
Рис. 2.63

На рисунке 2.63, приведенном выше, показана связь и различия между импульсной характеристикой интегрирующей rс-цепи и импульсной характеристикой цифрового фильтра, реализующего программу прохождения сигнала через данную интегрирующую rс-цепь. Реакция цифрового фильтра на «единичный импульс» - так называют дискретное представление δ(t)-функции - есть совокупность значений .

Рассмотрим прохождение прямоугольного импульса через интегрирующую rс-цепь в аналоговой и дискретной форме

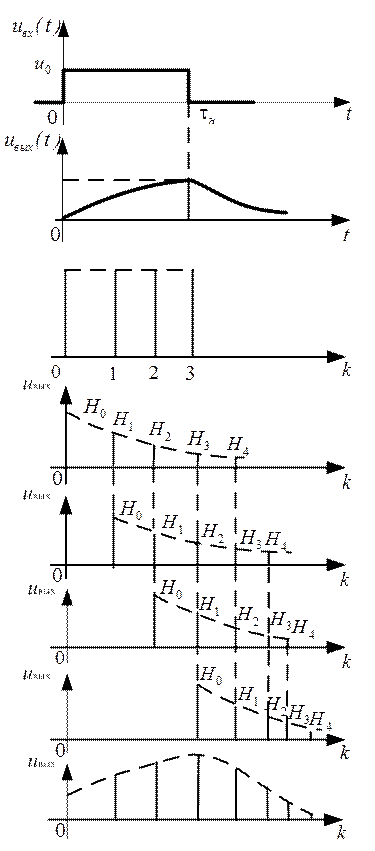
На рисунке 2.64 (сверху) показано изменение формы сигнала при прохождении через интегрирующую цепь. Аналогичные изменения формы будут иметь место и при прохождении через цифровой фильтр.

Дискретное представление прямоугольного видеоимпульса в виде 4х отсчетов (рис. 2.64(снизу)).

Дискретное представление отклика на "нулевой" отсчет.

Дискретное представление отклика на "первый" отсчет.

Дискретное представление отклика на "второй" отсчет.

Дискретное представление отклика на "третий" отсчет.

Дискретное представление отклика цифрового фильтра на прямоугольный видеоимпульс в дискретной форме.

Рис. 2.64

Как видно из приведенного рисунка отклик в 0-й момент времени состоит из реакции Н₀, в первый момент из суммы реакций на 0-й и 1-й отсчеты Н_о+Н₁, во второй момент времени из суммы реакций на 0-й, 1-й и 2-й отсчеты Н₀+Н₁+Н₂ и т.д. Для случая прямоугольного импульса все входные отсчеты одинаковы. Для произвольного сигнала необходимо учитывать неравенство входных отсчетов таким образом, чтобы реакция на данный отсчет H_i была взята с весом, пропорциональным входному сигналу в данный момент времени, реакция на предыдущий отсчет - с весом, пропорциональным входному сигналу в предыдущий момент времени и т.д., т.е.

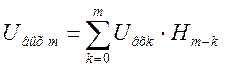, где m=0,1,2,…

Приведенная формула является дискретным аналогом интеграла Дюамеля с импульсной характеристикой.

Для ряда последовательных моментов времени будем иметь

и т.д., что соответствует геометрической интерпретации, приведенной на рисунках выше.

Смысл приведенного выше выражения прост и нагляден: для каждого входного отсчета цифровой фильтр проводит операцию взвешенного суммирования всех предыдущих значений входного сигнала, причем роль последовательности весовых коэффициентов играют отсчеты импульсной характеристики.

3. Общие сведения о спектральном методе анализа

3.1. Связь между спектрами сигналов на входе и на выходе линейной электрической цепи