Нестационарные процессы в электрических цепях, страница 10

Формирование импульса. С этой целью на сетку лампы подают положительный видеоимпульс определенной длительности и лампа открывается, её сопротивление резко падает до величины  и конденсатор  начинает разряжаться через модуляторную лампу на нагрузку (генератор СВЧ). На эквивалентной схеме это подключение на короткое время, равное длительности импульса, показана в виде замыкания и размыкания ключа. При этом разрядный ток будет протекать по замкнутой цепи: от положительно заряженной пластины конденсатора, через замкнутый ключ и сопротивление  (ключи  - лампа), через сопротивление  (генератора СВЧ) к отрицательно заряженной пластине конденсатора.

Через индуктивность , разрядный ток протекать практически не будет, т.к. разряд происходит за такое короткое время, что в этой индуктивности не успевает сколько-нибудь нарасти. За это время напряжение на накопительной ёмкости уменьшится по закону 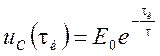 на величину .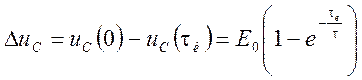

В связи с тем, что ,  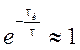и .

Возвращение в исходное состояние. После окончания действия отпирающего импульса разряд прекращается, т.к. модуляторная лампа запирается, после этого происходит дозаряд накопительной емкости  по пути: от " + " источника через сопротивление , через накопительную емкость , через зарядный дроссель  к " - " источника.

Эпюры напряжений показаны на рисунке 2.18

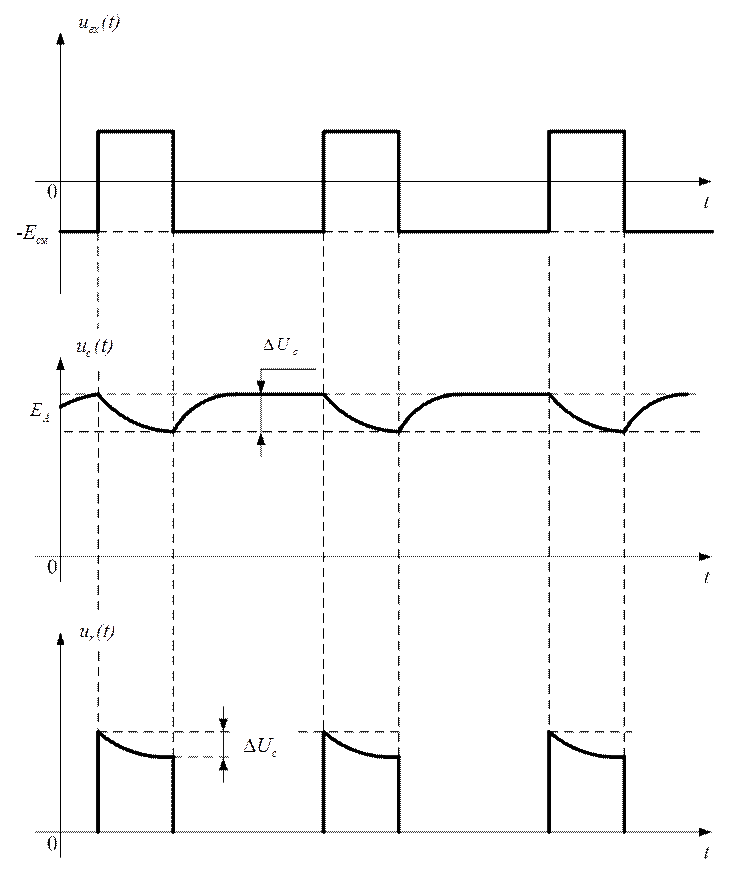
Рис.2.18

Напряжение на генераторный прибор будет подаваться только в те моменты времени, когда открыта модуляторная лампа. Под действием полученных мощных импульсов напряжения почти прямоугольной формы (периодическая последовательность видеоимпульсов почти прямоугольной формы) генераторный прибор формирует периодическую последовательность радиоимпульсов почти прямоугольной формы.

На принципиальной схеме показано, что параллельно  включен диод . Назначение его сводится к устранению отрицательного выброса напряжения на индуктивности , который возникает за счет того, что в  ответвляется часть разрядного тока и в момент запирания лампы этот ток скачком не прекращается, поэтому необходимо создать путь для его замыкания, для этой цели служит диод .

2.6. Переходные процессы в цепях второго порядка

2.6.1. Свободные процессы в цепях второго порядка

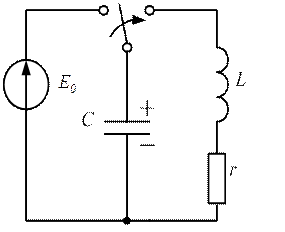Свободные процессы в (рис. 2.19) цепи будут иметь место при ненулевых начальных условиях, т.е. когда либо емкость, либо индуктивность, либо оба эти элемента содержат первоначальный запас энергии. На приведенном рисунке изображена схема, в которой имеется запас энергии в емкости .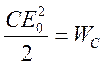

              Рис. 2.19

Качественный анализ процессов показывает, что при переключении ключа в правое положение будет иметь место разряд емкости через индуктивность , сопротивление . После разряда напряжение на емкости будет равно нулю. Наличие индуктивности вносит особенности в переходной процесс, которые заключаются в следующем: в отличие от свободных процессов в - цепи, где в начальный момент после коммутации ток будет иметь максимальное значение, влияние э.д.с. самоиндукции в индуктивности приводит к тому, что ток в цепи в начальный момент будет равен нулю (по I закону коммутации), а в дальнейшем будет иметь плавно возрастать до своего максимального значения. При этом, за счет протекания тока в индуктивности будет запасаться энергия, величина которой зависит от тока в данный момент 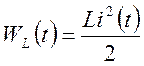. Часть энергии будет расходоваться в активном сопротивлении.

Процессы в данной цепи могут иметь различный характер в зависимости от соотношения между элементами цепи. Если добротность  данного контура будет меньше или равна 0,5 , то в этом случае, по мере разряда емкости до нулевого напряжения, произойдет рассеивание всей первоначально запасенной энергии на сопротивлении . Если , то в этом случае расход энергии на       сопротивлении  будет небольшой, и под действием э.д.с. самоиндукции, возникающей в индуктивности, будет протекать ток, перезаряжающий конденсатор. В этом случае напряжение на емкости будет противоположной полярности и несколько меньшего значения, чем  к концу полупериода перезаряда. В дальнейшем процесс будет повторяться вновь и вновь, пока вся запасенная энергия 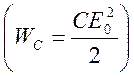 не израсходуется в активном сопротивление . Частота колебаний тока в цепи будет зависеть от величины емкости  и индуктивности .

Найдем аналитические выражения напряжения на емкости  и тока в цепи  согласно рассмотренному выше алгоритму.

1. Составление дифференциального уравнения.

По второму закону Кирхгофа, для цепи, сформированной в результате коммутации, имеем , применяя формулы связи, получим:

.

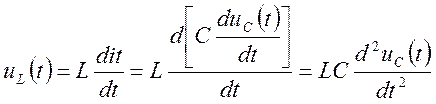
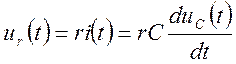
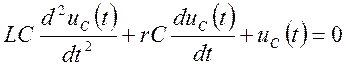2. Характеристическое уравнение цепи имеет вид:

 или ,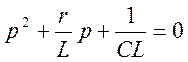

корни которого равны .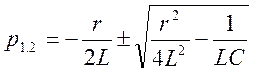

3. Определим начальные условия в цепи:

, .

4. Определим принужденные составляющие:

, .

5. Запишем искомую функцию  как сумму свободной и принужденной составляющих

,

а также первую производную этой функции:

.

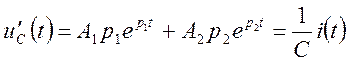Учитывая начальные условия цепи

,

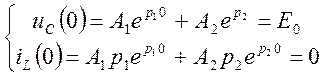получим систему уравнений для нахождения постоянных интегрирования  и

 

, .

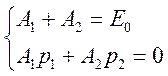
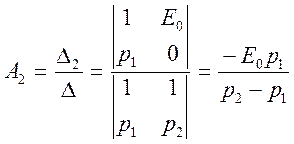6. Окончательное выражение искомой функции будет иметь вид

,

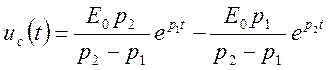а выражение для тока в цепи:

,

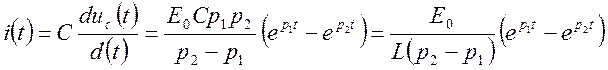т.к. по теореме Виета .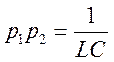

ПРИМЕЧАНИЕ*: Составляли и решали дифференциальное уравнение относительно , т.к. эта функция скачком не меняется, однако решение можно было найти и для  , т.к. ток в цепи также не меняется скачком.

Поведение функции  и  зависит от корней характеристического уравнения  и .

 Возможны два случая:

а) корни  и - вещественные;

б) корни  и  - комплексно-сопряженные.

Апериодический разряд емкости.

При малой добротности контура  в цепи будет иметь место апериодический разряд емкости т.к. корни  и  - вещественные и отрицательные, а также . Построим графики  и .

  График  получим, выполняя операцию графического дифференцирования функции , при этом учтем соображения:

- функция  - уменьшается, поэтому производная будет отрицательной;

- максимальное значение (по модулю) функции  будет тогда, когда  имеет максимальную крутизну.

Колебательный разряд емкости.

Колебательный разряд емкости происходит в случае, когда корни  и  являются комплексно-сопряженными. Введем следующие обозначения: