Нестационарные процессы в электрических цепях, страница 23

                       

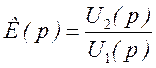
Рис. 4.10

Операторные передаточные функции электрической цепи К(р), также как и ее комплексные передаточные функции K(jω) и временные характеристики H(t) и G(t), не зависят от внешних воздействий на цепь. Они определяются только схемой цепи и параметрами входящих в нее элементов, т.е. характеризуют собственно цепь, и связаны между собой. Функция К(р) представляет собой определенную форму записи дифференциального уравнения цепи и является очень удобной характеристикой, определяющей динамические свойства цепи, т.е. свойства цепи в переходном режиме. Вследствие этого она нашла широкое применение при анализе систем автоматического управления.

Анализ переходных процессов в электрической цепи с помощью ее передаточной функции производят в следующем порядке:

1. По заданному входному сигналу u₁(t) находят его изображение U₁(р).

2. Определяют передаточную функцию цепи К(р).

3. Вычисляют изображение выходного сигнала с помощью соотношения

4. По изображению выходного сигнала U₂(р) определяют его оригинал u₂(t).

Если на вход цепи воздействует несколько сигналов, то применяется метод суперпозиции. Этот же метод используется и при ненулевых начальных условиях. Влияние начальных токов в индуктивностях и напряжений на емкостях учитывается как воздействие дополнительных сигналов, имеющих изображения  и .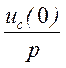

4.2.3. Связь передаточных функций с временными и частотными характеристиками цепей

Операторные передаточные функции К(р) электрической цепи, также как и ее комплексные частотные характеристики К(jω) и временные характеристики H(t) и G(t), не зависят от внешних воздействий на цепь. Они определяются только схемой цепи и параметрами входящих в нее элементов, т.е. характеризуют собственно электрическую цепь и, естественно, связаны между собой. Найдем эти связи.

Из сравнения формул для преобразования Лапласа и Фурье непосредственно следует, что

т.е. операторная передаточная функция К(р) получается из КЧХ  K(jω) путем замены оператора преобразования jω на более общий оператор. Поэтому для расчета К(р) по известной схеме цепи можно применить все методы расчета K(jω).

Связь между операторной передаточной функцией К(р) и временными характеристиками цепи H(t) и G(t), можно установить непосредственно из определения этих характеристик и связи между входной и выходной величинами.

Если на вход линейной электрической цепи подать воздействие в виде δ - функции δ(t), то реакция на выходе цепи будет ее импульсной характеристикой H(t). В операторной форме изображения входной и выходной функции на основании приведенной ранее таблицы можно записать

;          .

Следовательно импульсная характеристика определится

,

,

т.е. изображением импульсной характеристики цепи Н(t) является операторная передаточная функция К(р) или оригиналом К(р) является H(t).

При подаче на вход линейной электрической цепи единичной функции 1(t) на выходе получается переходная характеристика G(t). Как известно

.

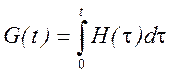Следовательно, изображение переходной характеристики G(p) на основании теоремы об интегрировании оригинала можно вычислить как

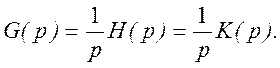
Отсюда переходная характеристика цепи связана с операторной передаточной функцией соотношением

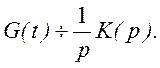
Полученные соотношения позволяют найти переходную G(t) и импульсную H(t) характеристики цепи по ее операторной передаточной функции.

Рассмотрим связь между передаточной операторной функцией и временными характеристиками цепи, приведенной на рисунке 4.11

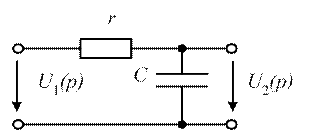
Операторная передаточная функция данной цепи по напряжению определяется в виде

  Рис. 4.11

                                                     где

Изображение импульсной характеристики следовательно равно

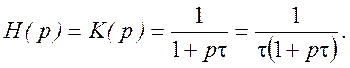
Воспользовавшись таблицей 4.1, получим импульсную характеристику цепи

.

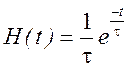Изображение переходной характеристики определится соотношением

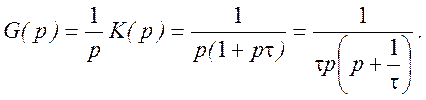
Отсюда переходная характеристика цепи может быть записана

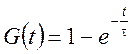
Полученные выражения совпадают с временными характеристиками интегрирующей цепи. С их помощью можно легко определить переходную G(t) или импульсную H(t) характеристику цепи по известной передаточной функции К(р).

5. Общие сведения о нелинейных электрических цепях

5.1. Особенности нелинейных цепей. Виды нелинейных элементов

В предыдущих разделах рассматривались линейные электрические цепи, состоящие из линейных элементов: резисторов, конденсаторов, катушек индуктивности, у которых соответственно сопротивление, емкость и индуктивность не зависят от величины приложенного напряжения или силы протекающего тока.

Однако, строго говоря, линейных элементов в технике не существует. Так, например, сопротивление резистора изменяется из-за нагрева током и становится нелинейным. Нелинейные характеристики имеют катушки индуктивности и конденсаторы.

Нелинейной цепью называется такая цепь, в состав которой входят нелинейные элементы.

Нелинейным элементом называется такой элемент, параметры которых зависят от приложенного напряжения или протекающего тока.

Различают следующие виды нелинейных элементов: нелинейные сопротивления, нелинейные емкости и нелинейные индуктивности.

Нелинейное сопротивление – это такой элемент, у которого активное сопротивление зависит от протекающего тока или приложенного напряжения. К числу нелинейных сопротивлений относят электронные лампы, ионные приборы, полупроводниковые диоды и триоды, тиристоры, динисторы.

Нелинейная ёмкость – это такой элемент, ёмкость которого зависит от величины приложенного напряжения. К ним относят варикапы, вариконды, у которых пространство между обкладками заполнено сегнетоэлектриком, электрическая проницаемость которого зависит от напряженности электрического поля.