Нестационарные процессы в электрических цепях, страница 3

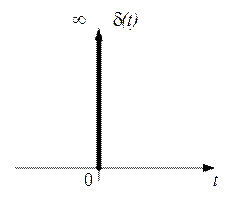
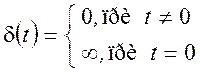
Рис. 1.23

Спектральную плотность получим путем вычисления интеграла

.

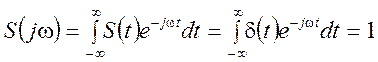Такой результат является следствием так называемого фильтрующего свойства дельта-функции(1.24), которое заключается в следующем

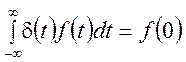, т. к. , то ,

         поэтому ,.

График спектра показанный на рисунке 1.25. Амплитудно – частотный спектр на всех частотах одинаков и равен 1. Фазочастотный спектр на всех частотах равен 0. АЧС является сплошным и ширина спектра бесконечна.

     

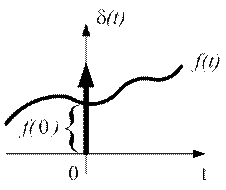
Рис.1.24

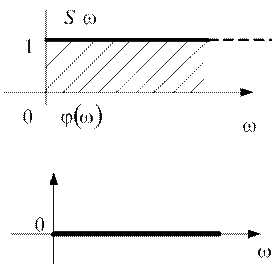
 Рис.1.25

Начальные фазы всех гармонических колебаний ( рис. 1.26) одинаковы и равны 0. Это значит, что в момент времени  = 0 все составляющие, изменяющиеся по косинусоидальному закону, проходят через амплитудное значение. В этот момент их сумма образует бесконечную величину.

                

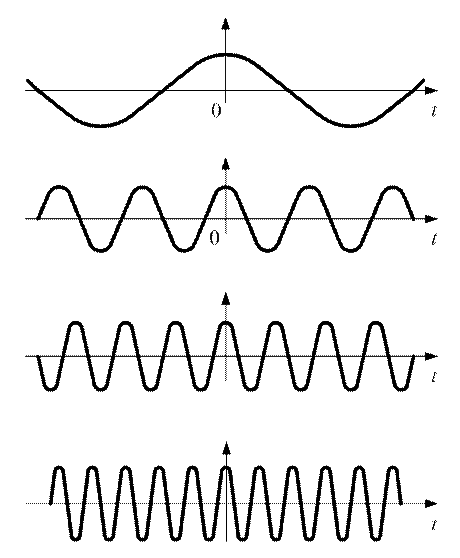
Рис.1.26

 Спектр функции включения

Функцией включения называется сигнал вида:

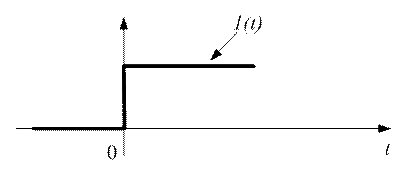
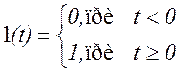
Рис. 1.27

Так как между функцией включения и дельта-функцией имеется связь

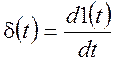                и                  ,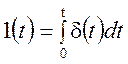

то для вычисления спектральной плотности функции включения можно воспользоваться теорией интегрирования, известной из курса математики, которая заключается в следующем:

если исходный сигнал  имеет спектральную плотность , то сигнал, полученный путем интегрирования исходного сигнала

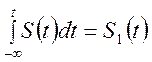
имеет спектральную плотность, вычисляемую как .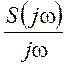

Другими словами, если ≓, то

≓.

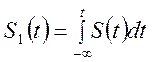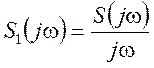Применяя теорему интегрирования для случая функции включения, имеем

, .

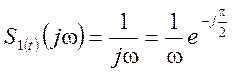Отсюда , .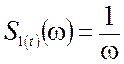

            

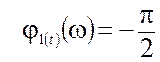Рис. 1.28

Спектр одиночного прямоугольного видеоимпульса (ОПВИ)

В связи с тем, что одиночный прямоугольный видеоимпульс (рис. 1.29) может быть представлен следующим образом

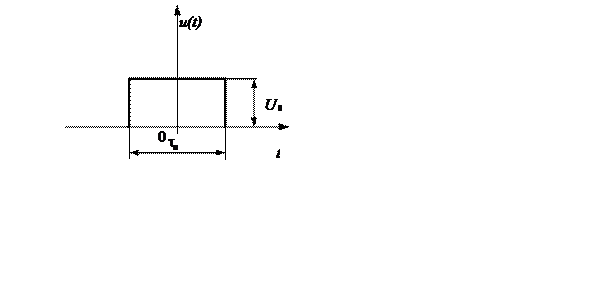
Рис.1.29

,

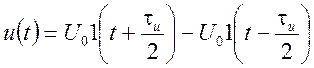то, используя свойство аддитивности преобразований Фурье, которое заключается в том, что если

≓, ≓ и т. д., то

≓

а также свойство сдвига аргумента состоящее в том, что если

≓, то ≓,

получим

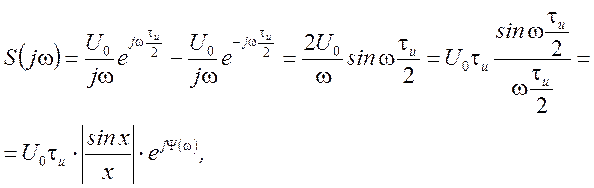
         где 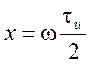 , а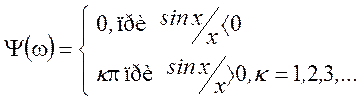

  Аналогичное выражение для  одиночного прямоугольного видеоимпульса получим, применяя интеграл Фурье

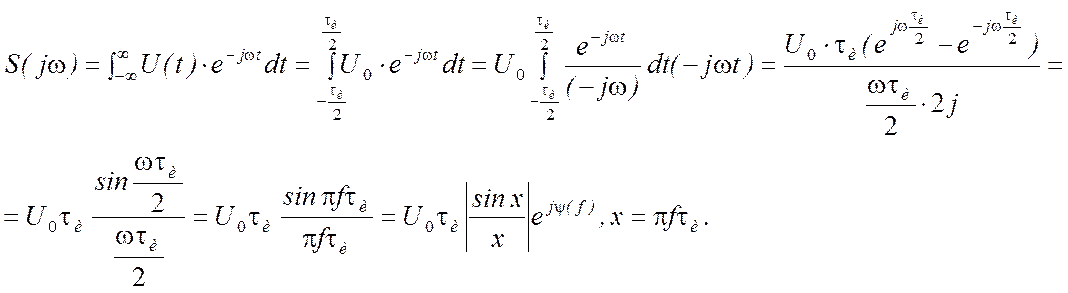
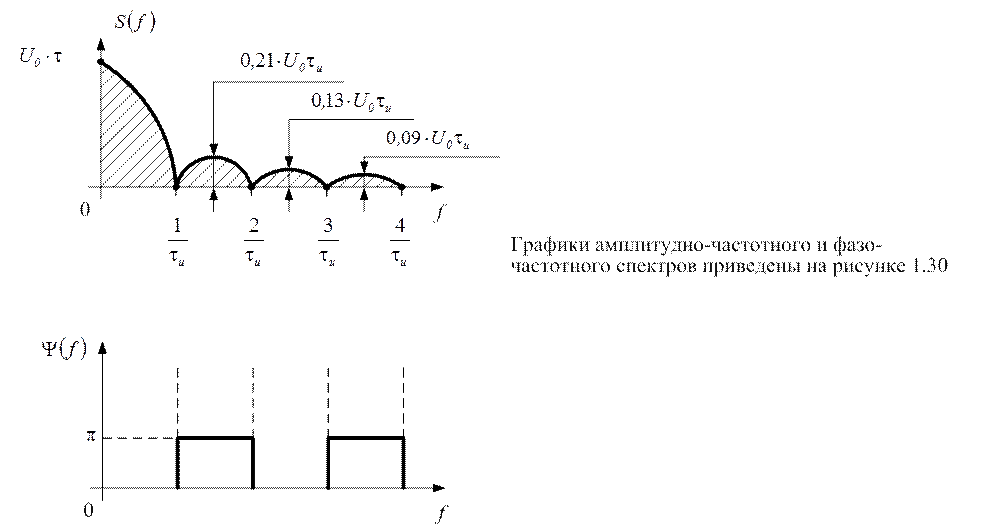
                                  Рис.1.30

Спектральная плотность зависит от частоты в соответствии с функцией  .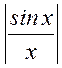  

Максимальное значение спектральной плотности при .

Нулевые значения спектральной плотности будут иметь место на частотах 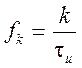, т.к. функция  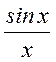проходит через ноль, когда ,где  = 1.2.3,.... т.е. на частотах

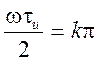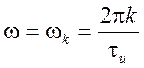,  или .

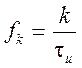Ширина спектра сигнала, определяемая на уровне 90% энергии сигнала (Э_с) равна 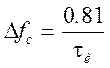. База сигнала .

График ФЧС построен исходя из следующих соображений. Положительным значением  соответствуют начальные фазы, равные нулю, а отрицательным - начальные фазы, равные .

Для оценки влияния длительности импульса на его спектр сравним АЧС импульсов разной длительности и одинаковой амплитуды. Длительность первого импульса , второго - .

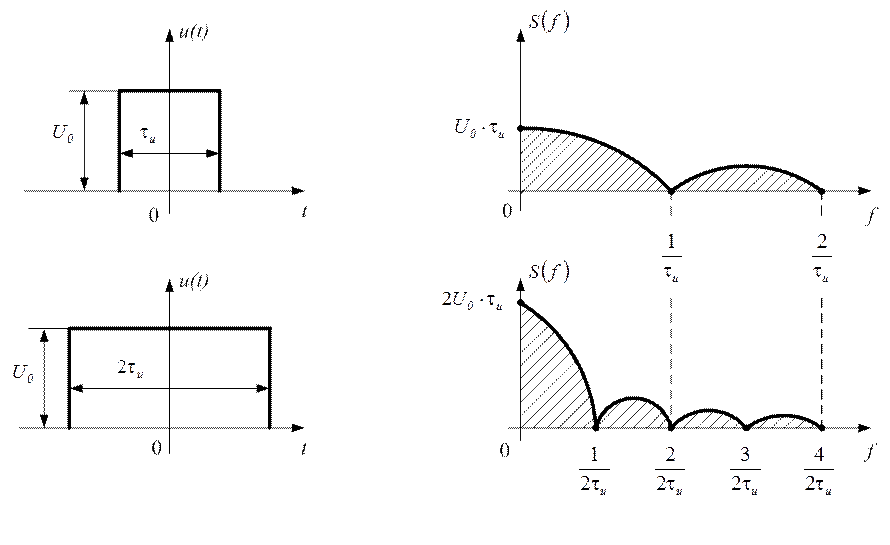
Рис. 1.31

Из анализа графиков  рисунка 1.31 следует, что удлинению импульса в 2 раза соответствует сужение графика АЧС, при этом ширина спектра уменьшается в 2 раза 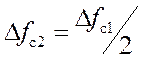, максимальное значение  пропорционально длительности импульса и увеличивается в 2 раза.

Для запаздывающего импульса, показанного на рисунке 1.6, спектральная плотность в соответствии с полученным выше результатом и теоремой о сдвиге аргумента будет

≓

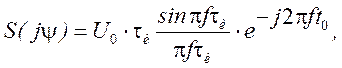
то есть при неизменном АЧС ФЧС определяется выражением

 .

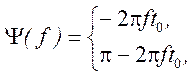
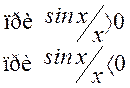График ФЧС при 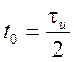 показан на рисунке 1.32

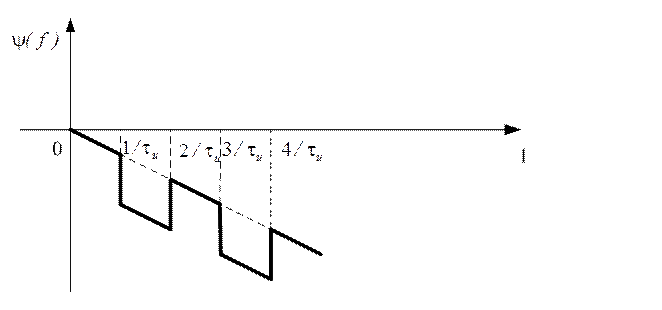
                Рис.1.32

Спектр видеоимпульса колоколообразной формы (ОКВИ)

 Огибающую выходного сигнала электрорадиотехнического устройства с ограниченной полосой пропускания можно аппроксимировать колоколообразной кривой. Кроме того огибающая колоколообразной формы формируется путем модуляции прямоугольной пачки прямоугольных радиоимпульсов, отраженных от цепи, диаграммой направленности антенной системой радиолокационной станции.

Рассматриваемый сигнал показан на рисунке 1.33.

 Он описывается выражением ,

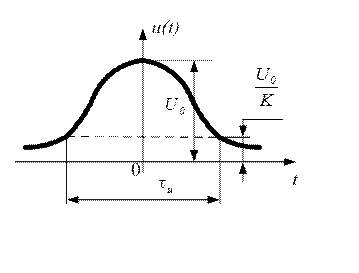 где - амплитуда импульса;

  - масштабный коэффициент

  .                                         

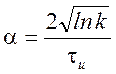                     Рис. 1.33

Для вычисления спектральной плотности применим интеграл Фурье 

.

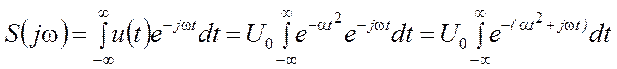Преобразуем показатель степени

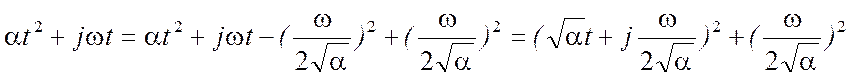
Обозначим

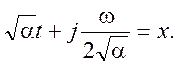
Тогда

 и 

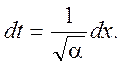
Получаем

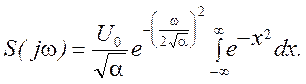
Полученный интеграл является табличным. Он носит название интеграла Лапласа и равен .

Следовательно

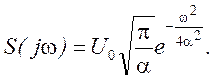
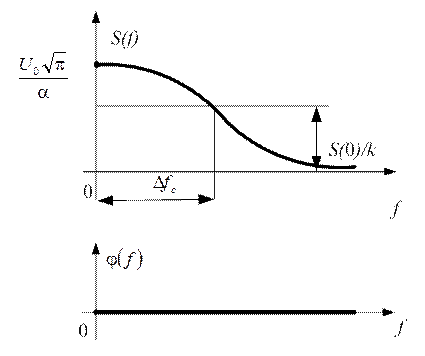 Графики АЧС и ФЧС, соответствующие выражению  приведены на рисунке 1.34

Анализ выражения показывает, что АЧС также имеет колокольную форму, а ФЧС равен нулю. Для оценки влияния длительности импульса на АЧС, сравним спектры сигналов одинаковой амплитуды и разной длительности.

Рис 1.34

Рис.1.35

Из анализа графиков рисунка 1.35 следует, что удлинению импульса соответствует сужение графика модуля спектральной плотности(уменьшению ширины спектра) и увеличение значения спектральной плотности в области низких частот.

Спектральная плотность при выбранном начале отчета времени получилась вещественной. Она так же, как и сам импульс, имеет колоколообразную форму. Коэффициент, определяющий длительность импульса входит в выражение  в знаменатели показателя степени. Поэтому, чем больше , что соответствует уменьшению длительности импульса и, таким образом, увеличивается ширина спектра сигнала, при этом уменьшается максимальное значение АЧС(S(0)) и наоборот.

Анализ графиков рисунка 1.34 показывает:

·  АЧС имеет сплошной спектр и имеет колоколообразную форму и сосредоточен в области низких частот.

·  Максимальное значение АЧС при f=0, 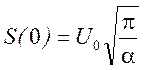 , и при k=e,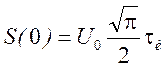

·  Ширина спектра на уровне 90% его энергии 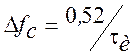( k=e)

·  ФЧС на всех частотах равен 0

·  База сигнала на уровне 90%  ширины спектра и длительности импульса .

 Спектр треугольного видеоимпульса

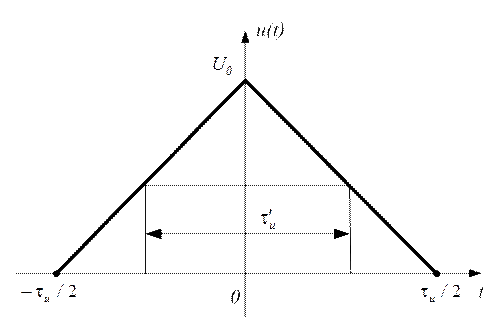
Треугольный видеоимпульс (рис 1.36) формируется на выходе радиоприемного устройства радиолокационной станции при оптимальной  обработке прямоугольных видеоимпульсов.

Рис. 1.36

Аналитическое выражение сигнала имеет вид

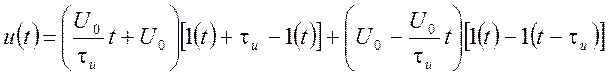, где .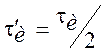

Спектральная плотность треугольного видеоимпульса определяется выражением

.

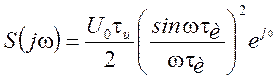График спектральной плотности приведен на рисунке 1.37