Нестационарные процессы в электрических цепях, страница 18

Еще меньшими значениями группового времени запаздывания сигналов характеризуются реактивные LC-фильтры нижних частот, используемые для задержки видеосигналов. Поясним это, воспользовавшись известным определением комплексного коэффициента передачи ФНЧ через его характеристическое затухание α(ω) и характеристическую фазу β(ω)

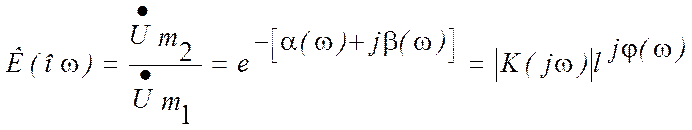
   где   

Получим аналитическое выражение, определяющее величину группового времени запаздывания сигналов в ФНЧ, используя известные для этого фильтра соотношения

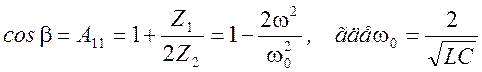
Отсюда

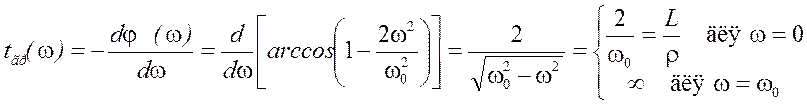
График зависимости t_гр(ω), которую называют дисперсионной характеристикой, показан на рисунке 3.8. Видим, что в пределах почти всей полосы пропускания ФНЧ имеет равномерную зависимость |K(jω)|  и почти постоянное время групповой задержки. Это свойство ФНЧ и определяет его широкое применение в качестве линии задержки для видеосигналов. Чтобы получить при этом требуемое время задержки, включают по цепной схеме К одинаковых звеньев ФНЧ.

Тогда время задержки увеличивается в К раз. Такие цепи обычно рассчитываются на время задержки от нескольких десятков наносекунд до нескольких микросекунд.

3.4.3. Понятие о сжатии ЛЧМ и ФМ сигналов РЭТ

Как следует из анализа дисперсионной характеристики ФНЧ, в диапазоне частот от ω' до ω" этот фильтр можно использовать для сжатия во времени сигналов с внутриимпульсной линейной частотной модуляцией. Поясним эту возможность, используя квазистационарный метод анализа.

 Будем полагать, что величина выбранного интервала частот

равна девиации частоты Δω_g ЛЧМ сигнала, а соответствующее этому интервалу частот изменение группового времени задержки

равно длительности τ_u ЛЧМ сигнала. Считаем также, что выход генератора ЛЧМ сигналов соединен непосредственно со входом фильтра (т.е. дополнительной задержки сигналов в цепи нет), а мгновенная частота, ω_ЛЧМ(t) сигнала уменьшается с течением времени. Здесь же приведен и выбранный участок дисперсионной характеристики фильтра.

Разобьем входной сигнал и выбранный участок дисперсионной характеристики на m равных частей и заменим линейные зависимости ω_ЛЧМ(t) и t_гр(ω) ступеньчатыми, как на рисунке. Найдем, в какие моменты времени появятся на выходе фильтра каждый из парциальных радиоимпульсов длительностью 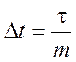полученных в результате такого преобразования.

Первый импульс поступает на вход фильтра в момент времени, а величина его задержки в фильтре, определяемая частотой ω₁ несущего колебания этого радиоимпульса, равна, как видно из рисунка значению

Поэтому на выходе фильтра первый импульс появится в момент времени t₁ равный

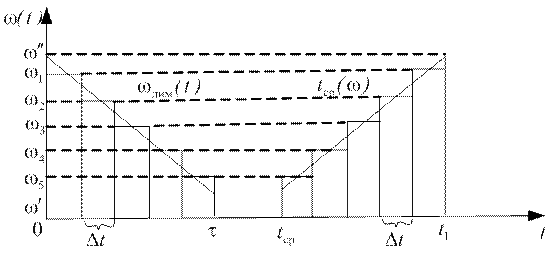
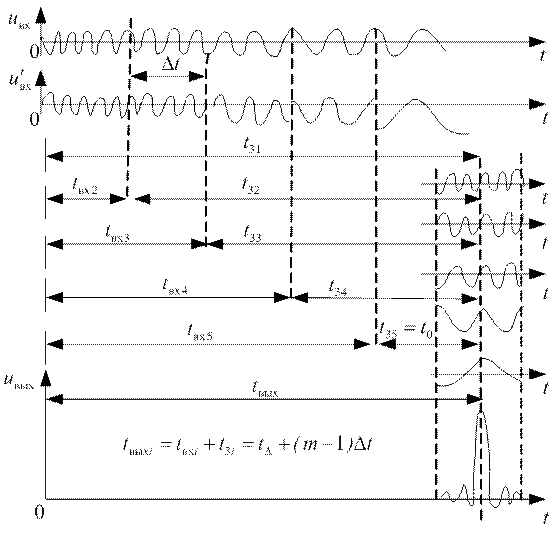
Рис. 3.9

Следующий парциальный радиоимпульс, как видно из рисунка 3.9,   имея частоту несущего колебания ω₂, поступает на вход фильтра в момент времени , a задерживается в нем на время t₃₂, равное

значит на выходе фильтра он появится в момент времени

В результате аналогичных рассуждений получим, что все парциальные импульсы появляются на выходе фильтра в один и тот же момент времени

.

В результате суммирования этих m парциальных импульсов формируется выходной сигнал, амплитуда которого в m раз больше амплитуды парциальных импульсов, а его длительность меньше длительности парциальных импульсов, а значит в m раз меньше длительности исходного ЛЧМ сигнала. Этот эффект более наглядно иллюстрируется рисунком, где показаны входной сигнал с внутриимпульсной линейной частотной модуляцией, результат его замены совокупностью пристыкованных друг к другу m парциальных радиоимпульсов с частотами несущего колебания ω₁, ω₂,… совокупность появившихся одновременно на выходе фильтра Ф парциальных импульсов и сформированный в результате их суммирования выходной сигнал.

Чтобы суммарный спектр парциальных радиоимпульсов точнее воспроизводил спектр входного сигнала, спектры парциальных импульсов должны соприкасаться, но не перекрываться. Это будет при условии

,

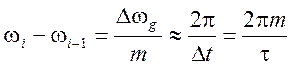отсюда следует, что

,

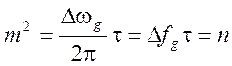где       n - коэффициент широкополосности ЛЧМ сигнала.

Таким образом, амплитуда выходного сигнала фильтра увеличилась в  раз, а его длительность уменьшилась в n раз по сравнению с соответствующими параметрами входного сигнала. Полученный результат полностью совпадает с результатом точного анализа процессов в цепи с линейным участком дисперсионной характеристики. В качестве такой цепи используется, естественно, не один фильтр нижних частот, а линия задержки, содержащая большое количество таких фильтров. Их параметры рассчитываются таким образом, чтобы как можно больше увеличить частотные и временные размеры участка суммарной дисперсионной характеристики, пригодного для сжатия ЛЧМ сигналов. Если все параметры такого участка дисперсионной характеристики линии задержки согласованны (равны) с соответствующими параметрами поступающих на вход ЛЧМ сигналов, то линия называется согласованным или оптимальным фильтром для этих сигналов.

Используя линии задержки, можно реализовать и устройства, предназначенные для сжатия во времени сигналов с внутриимпульсной фазовой манипуляцией, т.е. их согласованные (оптимальные фильтры). В качестве примера на стр.121 показана схема такого устройства, предназначенного для сжатия во времени фазоманипулированного сигнала, закодированного в соответствии c 7-значным кодом Байкера.

Как видно из рисунка, согласованный фильтр для фазоманипули-рованного сигнала состоит из линии задержки ЛЗ, фазоинверторов ФИ, сумматора и фильтра, параметры которого согласованны с параметрами парциальных импульсов входного сигнала. Линия задержки имеет отводы, с

которых снимаются сигналы, полностью повторяющие входной сигнал, но задержанные относительно него на время

где       Δt - длительность парциальных импульсов входного сигнала,

N - число парциальных импульсов во входном сигнале.