Нестационарные процессы в электрических цепях, страница 6

4)  Ширина спектра сигнала на уровне 90% его энергии .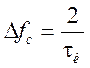

5)  ФЧС гармоник в пределах центрального и четных лепестков равен , в пределах нечетных .

6)  База сигнала при ширине спектра, определенного на уровне 90% его энергии, .

1.4.3. Радиосигнал с однотональной угловой модуляцией

Принципы, лежащие в основе угловой модуляции, были выдвинуты Гельмгольцем в 1862 году задолго до развития радиотехники. Однако впервые она была применена в радиосвязи в 1912г.

Различают частотную модуляцию и фазовую модуляцию. При фазовой модуляции (ФМ) модулирующая функция воздействует на начальную фазу несущего колебания. При частотной модуляции (ЧМ) модулирующая функция действует на частоту несущего колебания.

Как известно, угловая частота в общем случае есть скорость изменения полной фазы, т.е.

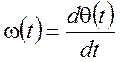, где -полная фаза.

Это значит, что если при ФМ фазовый угол  пропорционален модулирующей функции

,  - коэффициент пропорциональности,

то соответствующая мгновенная частота

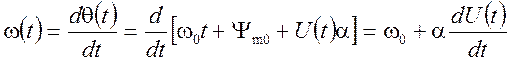
пропорциональна производной сигнала, и наоборот, при ЧМ мгновенная частота пропорциональна модулирующему сигналу

, - коэффициент пропорциональности,

а начальная фаза пропорциональна его интегралу

.

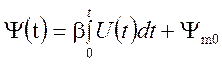При угловой модуляции амплитуда ФМ и ЧМ колебаний остается неизменной, что повышает экономичность работы радиопередатчиков, использующих УМ и позволяет улучшить помехоустойчивость при использовании ФМ и ЧМ.

При анализе спектров ограничимся рассмотрением простейшего случая угловой модуляции по синусоидальному закону:

,

где М - индекс угловой модуляции;

       - угловая частота модулирующего колебания.

График такого колебания показан на рисунке 1.54

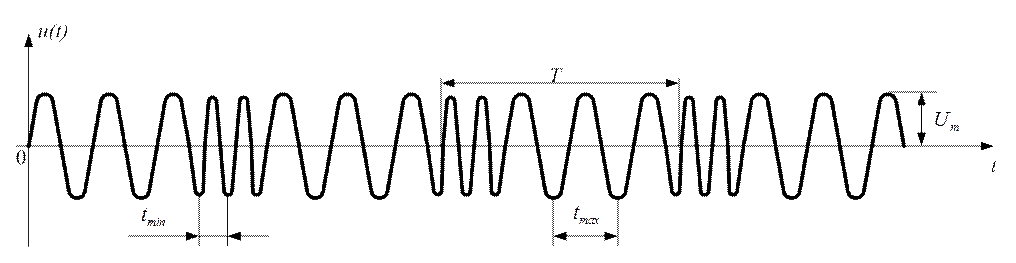Рис. 1.54

Из анализа графика следует, что с течением времени происходит изменение периода (частоты) несущего колебания, это изменение происходит по закону:

.

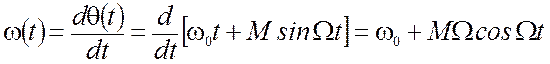Пределы изменения частоты от до . Величина   - называется девиацией частоты. Анализ спектра такого колебания достаточно сложен, поэтому приведем окончательное выражение

.

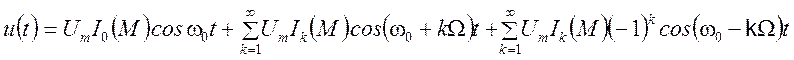Здесь - значение функции Бесселя первого рода к-го порядка, вычисленное при заданном значении М;

М - индекс угловой модуляции.

Как видно из приведенного выражения, спектр радиосигнала с однотональной угловой модуляцией имеет бесконечное число пар боковых составляющих. На практике число спектральных составляющих определяется значением индекса угловой модуляции. Из анализа графиков функции Бесселя следует, что чем больше порядок функции Бесселя, тем при большом значении М появляются её значения, отличные от нуля. Например, при М =4 заметно отличаются от нуля только функции;

; ; ; ; ;

Можно считать, что каждая боковая полоса при М = 4 содержит по 5 составляющих, комплексные амплитуды которых находят как

а) для левой боковой полосы:               б) для правой боковой полосы:

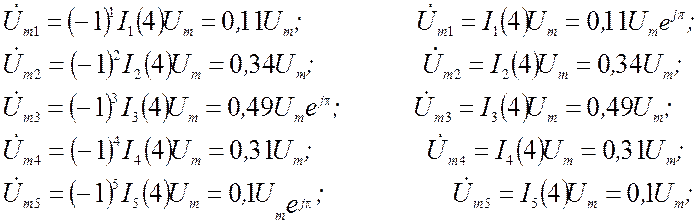
а комплексную амплитуду несущего колебания

.

Исходя из данных, полученных в результате расчетов нетрудно построить АЧС и ФЧС этого сигнала, АЧС и ФЧС показаны на рисунке 1.55

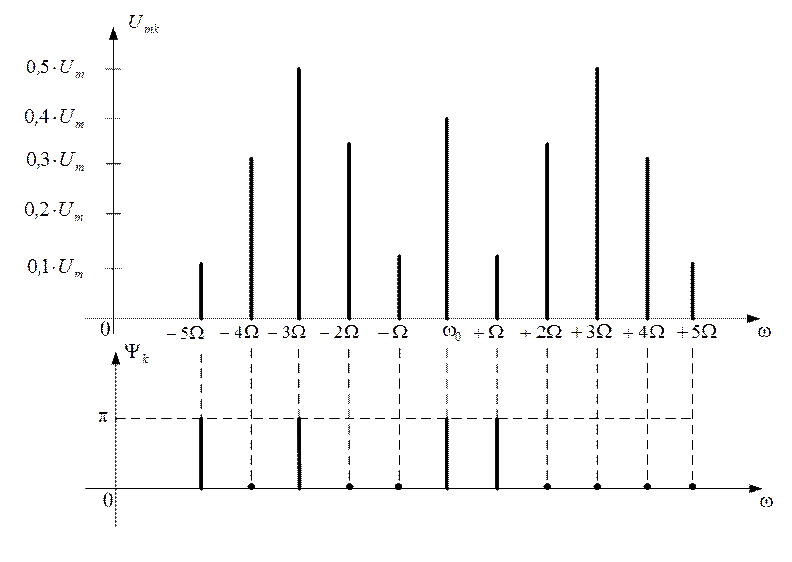
Рис. 1.55

Из анализа рисунков видно, что АЧС симметричен относительно несущего колебания, а в ФЧС нечетные составляющие противофазны, а четные находятся в фазе.

Анализ спектров показывает, что с увеличением индекса М число спектральных составляющих увеличивается, причем их число примерно равно 2М+3, а область частот, занимаемая сигналом примерно равна .

Влияние М и   показано соответственно на рисунке 1.56 и рисунке 1.57

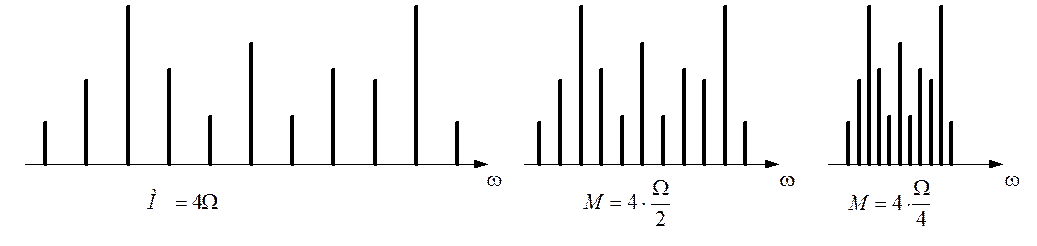Рис. 1.54

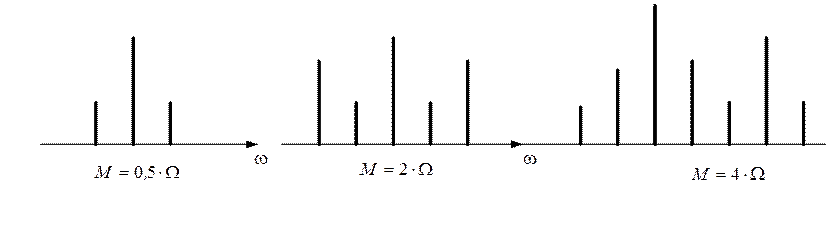 Рис.1.55

1.5. Сложные сигналы и их спектры

1.5.1. Пачки импульсов

На практике широко используются пачки импульсов. Например, при обзоре радиолокатором цепи от нее отражается и поступает на вход приемника последовательность из определенного числа импульсов, следующих через равные промежутки времени.

Пачкой импульсов называют ограниченную во времени последовательность импульсов одинаковой формы. Закон изменения величины импульсов в пачке называют её огибающей.

Колокольная пачка прямоугольных видеоимпульсов

Такая пачка может быть получена путем амплитудной модуляции по закону - периодической последовательности прямоугольных видеоимпульсов (рис. 1.58).

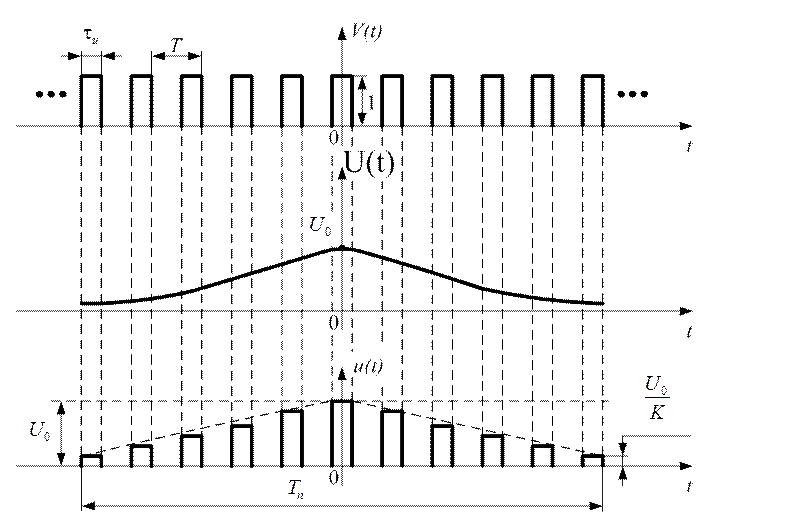
Рис. 1.58

Как видно из рисунка 1.58результирующий сигнал получен путём перемножения модулирующей функции на несущую

, где

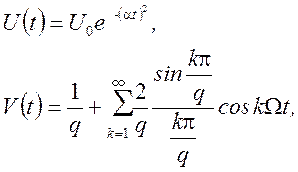
поэтому сигнал можно записать

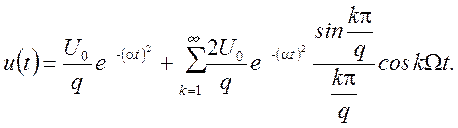
Как видно из полученного выражения, искомый сигнал является совокупностью видео и радиоимпульсов различной амплитуды, одинаковой длительности равной  и различной частоты . Например

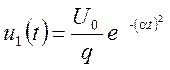- видеоимпульс

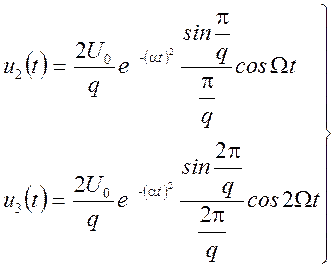- радиоимпульсы и т.д.

Спектральные плотности импульсов  и т.д. были получены ранее, поэтому спектральную плотность колокольной пачки прямоугольных видеоимпульсов можно записать, воспользовавшись аддитивным свойством ряда Фурье: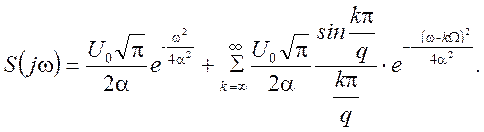           

Из приведенного выражения видно, что спектр пачки состоит из спектров импульсов колокольной формы, амплитуды которых зависят от множителя 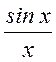 , а частоты равны .

АЧС колокольной пачки прямоугольных видеоимпульсов изображён на рисунке 1.59

Рис. 1.59

Этот график наглядно иллюстрирует тот факт, что спектральные параметры сигнала обратно пропорциональны временным параметрам. Из анализа графика АЧС следует, что:

- длительность импульса определяет ширину каждой арки спектра;

- длительность периода определяет разность частот, на которую отстоят друг от друга спектральные лепестки;

(указанные два параметра принадлежат периодической последовательности, поэтому спектр пачки внешне похож на спектр периодической последовательности прямоугольных видеоимпульсов)

- длительность пачки определяет ширину спектра одного лепестка.

Анализ приведенного спектра показывает, что длительные пачки обладают амплитудно-частотными спектрами с узкими лепестками и наоборот, ширина лепестков коротких пачек велика.

Прямоугольная пачка прямоугольных видеоимпульсов

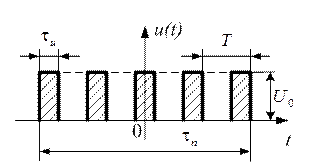
На рисунке 1.60 приведена прямоугольная пачка прямоугольных видеоимпульсов.

Рис. 1.60

Спектр такой пачки будет отличаться от спектра колокольной пачки формой лепестков. На рисунке 1.61 приведена зависимость АЧС от длительности пачки.