Нестационарные процессы в электрических цепях, страница 5

b) Частота к-ой гармоники осталось неизменной ;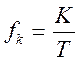

с) Ширина спектра сигнала на уровне  90% его энергии уменьшилась в 2 раза ;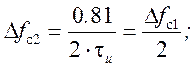

d) Постоянная составляющая увеличилась в 2 раза

Таким образом, можно сделать вывод, что при увеличении длительности импульса, происходит “сжатие” АЧС вдоль оси ординат (уменьшается ширина спектра сигнала), при этом увеличиваются амплитуды спектральных составляющих. Частоты гармоник не изменяются.

На рисунке 1.44. представлен пример изменения сигнала и его  АЧС при увеличении периода следования в 4 раза (уменьшение частоты повторения в 4 раза).

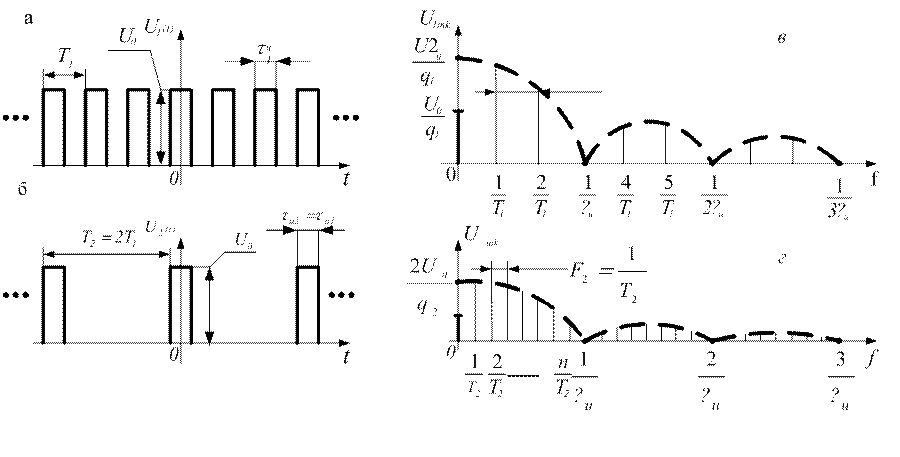Рис. 1.45

Из анализа приведенных графиков следует:

1)  Для ПППВИ с периодом :

          а) скважность =2, следовательно в пределах каждого лепестка находится 1 гармоника;                                                  

      б) частота к-ой гармоники ;

      в) ширина спектра сигнала на уровне 90% его энергии  г) постоянная составляющая равна .

2)  Для ПППВИ с периодом =4:

а) скважность =4, следовательно, в пределах каждого лепестка    сосредоточено 3 гармоник;

б) частота к-ой гармоники уменьшилась в 4 раза;

в) ширина спектра сигнала на уровне 90% его энергии 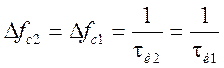    не изменилась;

г) постоянная составляющая  уменьшилась в 4 раза.

Таким образом, можно сделать вывод, что при увеличении периода следования (уменьшении частоты повторения происходит “сжатие ”) АЧС вдоль оси частот (уменьшаются амплитуды гармоник с увеличением их количества в пределах каждого лепестка). Ширина спектра сигнала при этом не изменяется. Дальнейшее уменьшение частоты повторения (увеличения периода следования ) приведет (при ) к уменьшению амплитуд гармоник до бесконечно малых величин. При этом сигнал превратиться в одиночный, соответственно спектр станет сплошным.

1.4. ПЕРЕОДИЧЕСКИЕ РАДИОСИГНАЛЫ И ИХ СПЕКТРЫ

1.4.1. Радиосигнал с однотональной амплитудной модуляцией

При амплитудной модуляции (AM) амплитуда несущего синусоидального колебания подвергается воздействию модулирующей функции(рис. 1.46).

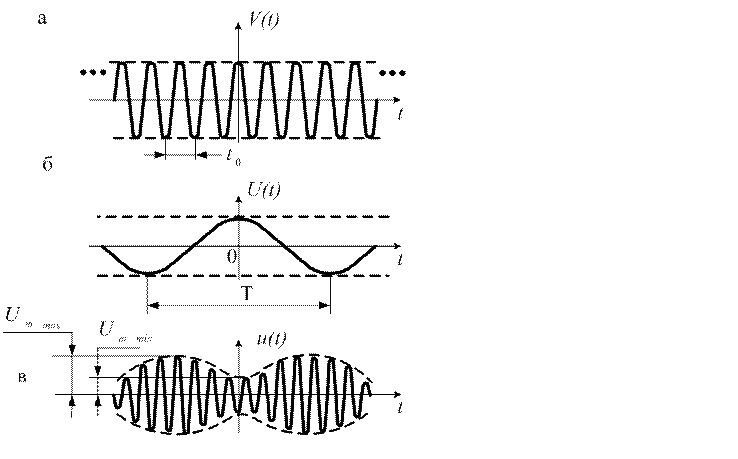
Рис. 1.46

Аналитическое выражение несущего колебания имеет вид:

 где , .

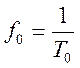Аналитическое выражение модулирующего колебания определяется выражением:

 где , .

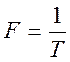Мгновенное значение радиосигнала с однотональной AM определяется выражением:

,

где:

;

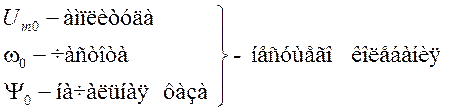- "переменная амплитуда";

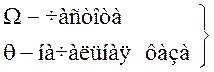 - модулирущей функции;

- коэффициент модуляции или коэффициент глубины модуляции,

 

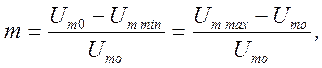
Для определения спектра однотонального АМ сигнала проведем тригонометрические преобразования:

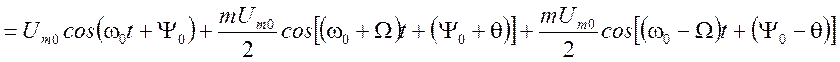          Как видно из приведенного выражения спектр сигнала состоит из трех составляющих: одной - с частотой несущего колебания  и двух других - с частотами и .

Графики АЧС и ФЧС приведены на рисунке 1.47. Сравнивая полученный спектр со спектром несущего колебания, заметим, что модуляция приводит к появлению двух новых колебаний с боковыми частотами .

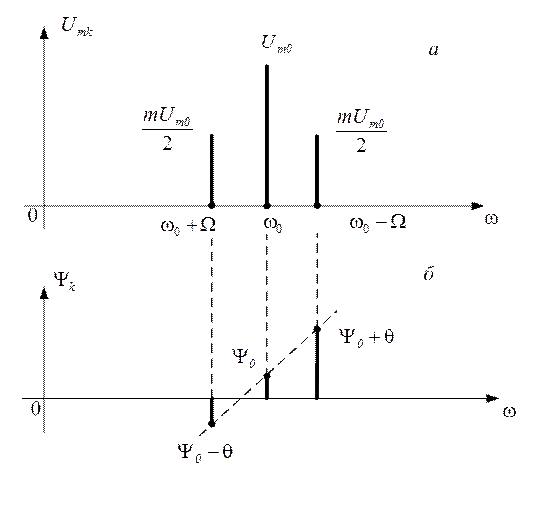
Рис. 1.47

 Амплитуды этих колебаний 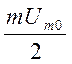   зависят от коэффициента модуляции .

Выражения для мгновенного значения амплитудно-модулированного сигнала при модуляции несколькими частотами имеет вид

.

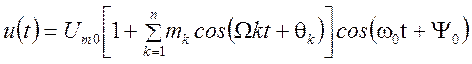Выполняя аналогичные тригонометрические преобразования получим спектр этого сигнала

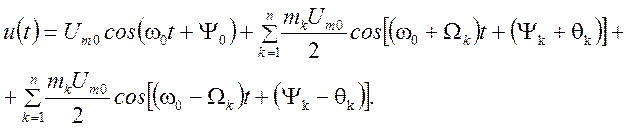
Амплитудно-частотный спектр этого колебания изображен на рисунке 1.48

Рис. 1.48

Он состоит из несущего колебания и составляющих нижней и верхней боковых полос спектра.

Радиосигнал с однотональной амплитудной модуляцией с подавленной несущей

Аналитическое выражение такого сигнала имеет вид

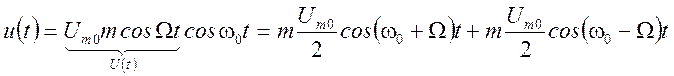
Графики сигнала (рис. 1.49) и спектра (рис. 1.50) приведены ниже

Если к приведенным графикам прибавить несущее колебания получим радиосигнал с однотональной амплитудной модуляцией, рассмотренный ранее (рис.1.46).

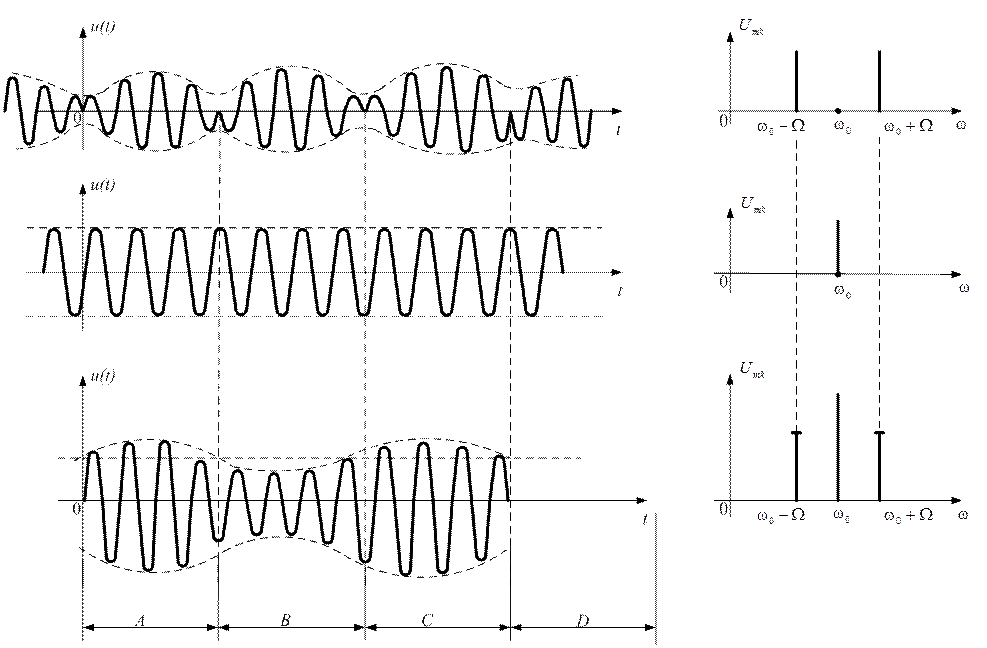
Рис. 1.51

Сложение колебаний на участках А и С происходит в фазе, а на участках В и Д - в противофазе, поэтому имеет место пульсация амплитуды колебаний от  до , а для АМ сигнала, а для AM сигнала с подавленной несущей амплитуда колеблется от 0 до . АМ сигналы с подавленной несущей находят широкое применение в радиотехнике.

1.4.2. Периодическая последовательность прямоугольных радиоимпульсов (ПППРИ)

Как отмечалось ранее, ПППРИ применяется в качестве зондирующих сигналов в РЛС для обнаружения и измерения координат целей; в качестве несущих функций в электросвязях.

Один из способов получения периодической последовательности прямоугольных радиоимпульсов является применения амплитудной модуляции. При этом, в качестве несущей функции используется гармоническое колебание , модулирующей функцией является периодическая последовательность прямоугольных видеоимпульсов, аналитическое выражение которой при разложении ее в ряд Фурье имеет вид .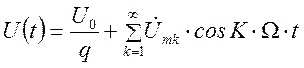

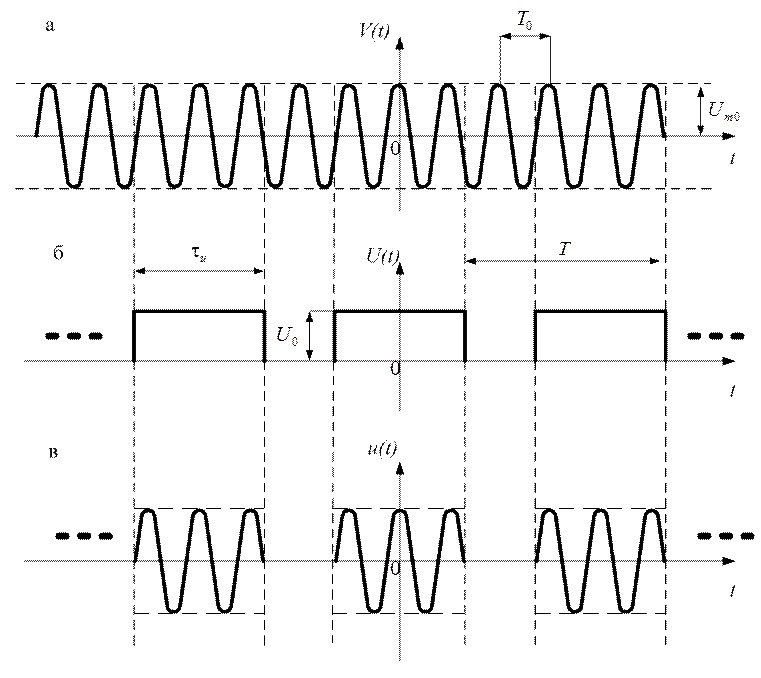
Рис. 1.52

Модулирующая функция во временной области изображена на рисунке 1.52 б, а ПППРИ - на рисунке 1.52 в. Аналитическое выражение ПППРИ в данном случае определяется выражением .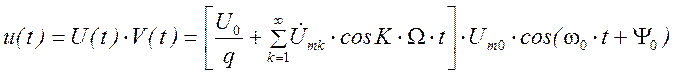

Произведя умножение модулирующей на несущую функцию, и тригонометрические преобразования (примем ) аналитическое выражение u(t) имеет вид:

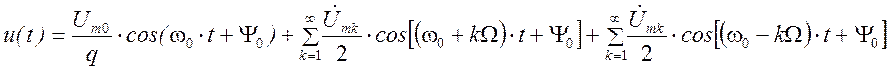где 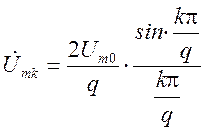- амплитуда к-ой гармоники периодической последовательности прямоугольных рассчитанная ранее, в которой  заменено на . Из анализа поученного результата следует, что АЧС ПППРИ имеет вид (рис. 1.53.а), ФЧС изображен на (рис. 1.53.б).

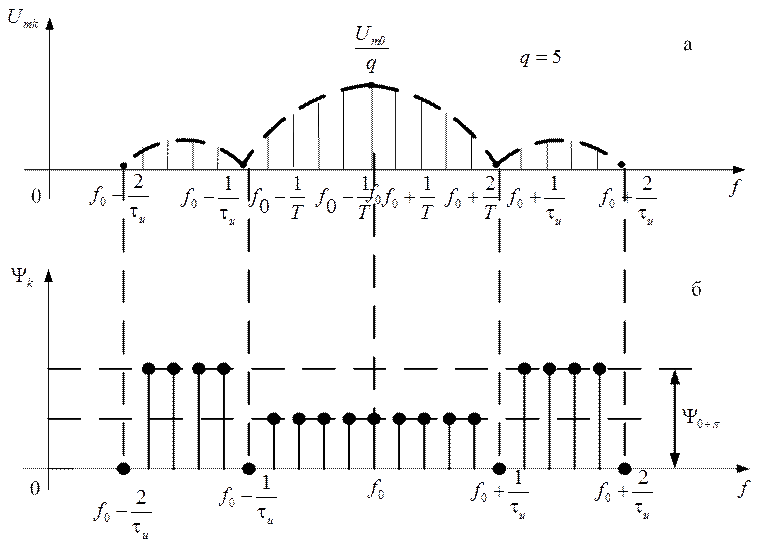
Рис. 1.53

Анализ полученных результатов позволяет сделать следующие выводы:

1)  Спектр дискретный и состоит из:

a)  гармоники с  и амплитудой  ;

b)  верхней боковой полосы частот ( ВБП) гармоники  и амплитуды ;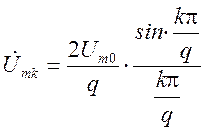

c)  Нижней боковой полосы частот (НБП) гармоники, частоты которых , с амплитудами соответствующим амплитудам ВБП частот (при одинаковом значении k);

2)  Распределение амплитуд гармоник по величине подчиняются закону . При этом амплитуды гармоник пропорциональны амплитуде импульсов и уменьшаются с ростом их скважности, что объясняется физически уменьшением энергии в импульсе.

3)  В пределах каждого лепестка, кроме центрального, сосредоточено q-1 гармоник, в центральном 2q-1.