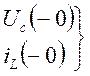 напряжение и ток в момент непосредственно перед коммутацией,
напряжение и ток в момент непосредственно перед коммутацией,
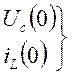 напряжение и ток в момент коммутации,
напряжение и ток в момент коммутации,
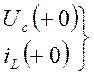 напряжение и ток непосредственно после коммутации.
напряжение и ток непосредственно после коммутации.
Сформулируем законы коммутации:
![]() - ток в индуктивности скачком не изменяется.
- ток в индуктивности скачком не изменяется.
![]() -
напряжение на емкости скачком не изменяется.
-
напряжение на емкости скачком не изменяется.
Начальными условиями называют значения токов в индуктивностях и напряжений на емкостях непосредственно до коммутации. Различают нулевые и ненулевые начальные условия.
ПРИМЕР I. Определить начальные
условия в цепи (рис. 2.2). Напряжение на емкости до коммутации было равно нулю,
поэтому ![]() - нулевые начальные условия.
- нулевые начальные условия.
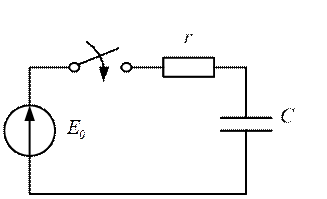
Рис. 2.2
ПРИМЕР 2.
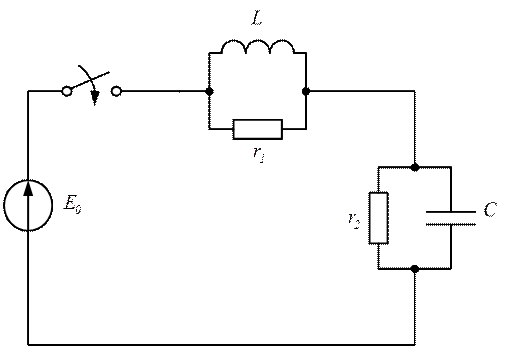
Определить начальные условия (рис. 2.3). До коммутации в
цепи протекал ток по цепи: от "+" источника через ключ, индуктивность
![]() , сопротивление
, сопротивление ![]() к "-" источника.
к "-" источника.
Рис. 2.3
При этом, по закону Ома ток в цепи равен: 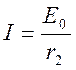 ,
,
а напряжение на емкости равно ![]()
Вывод: 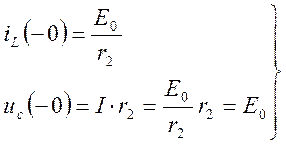 ненулевые начальные условия
ненулевые начальные условия
2.2. Алгоритм составления и решения дифференциальных уравнений электрических цепей
При анализе переходных процессов классическим методом составляют уравнений для мгновенных значений токов и напряжений. Эти уравнения составляют по законам Кирхгофа (как правило), при этом используют соотношения между токами и напряжениями для элементов цепи.
![]()
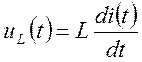 ;
;
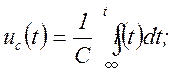
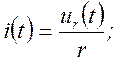
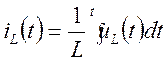 ;
;
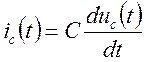
Рассмотрим пример составления дифференциального уравнения цепи, приведенной на рисунке 2.4. Согласно II закону Кирхгофа для любого момента времени в этой цепи имеем
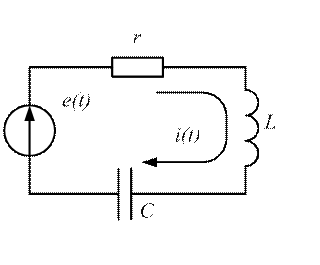
Рис. 2.4
![]() .
.
Это уравнение необходимо преобразовать так, чтобы в него
входила только одна искомая функция - ток или напряжение: ![]() или
или ![]() .
.
Подставляя приведенные выше соотношения, получим:
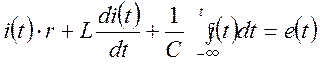 .
.
Продифференцировав это уравнение по ![]() ,
и разделив правую и левую части равенства на
,
и разделив правую и левую части равенства на ![]() ,
получим линейное дифференциальное уравнение второго порядка
,
получим линейное дифференциальное уравнение второго порядка
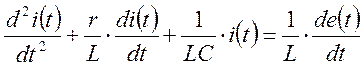 .
.
Можно показать, что порядок дифференциального уравнения одноконтурной цепи определяется числом разнотипных накопительных элементов.
Решение дифференциального уравнения может быть представлено в виде
![]() ,
,
где ![]() - свободная составляющая - общее решение
однородного дифференциального уравнения (без правой части),
- свободная составляющая - общее решение
однородного дифференциального уравнения (без правой части),
![]() - принужденная составляющая, рассчитывается в
установившимся режиме (t=
- принужденная составляющая, рассчитывается в
установившимся режиме (t=![]() ).
).
Свободную составляющую ![]() обычно
находят в виде суммы экспоненциальных функций:
обычно
находят в виде суммы экспоненциальных функций:
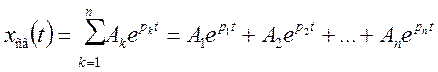 ,
,
где ![]() - порядок
дифференциального уравнения,
- порядок
дифференциального уравнения,
![]() - постоянные
интегрирования,
- постоянные
интегрирования,
![]() - корни
характеристического уравнения, получаемого из дифференциального уравнения путем
замены
- корни
характеристического уравнения, получаемого из дифференциального уравнения путем
замены
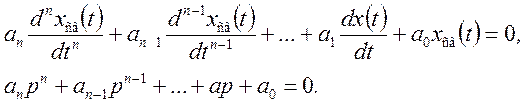
Корни характеристического уравнения для пассивных
электрических цепей могут быть либо отрицательными, либо
комплексно-сопряженными с отрицательной вещественной частью. Поэтому ![]() при
при ![]() стремится
к нулю. Следовательно, решение дифференциального уравнения при
стремится
к нулю. Следовательно, решение дифференциального уравнения при ![]() стремится к
стремится к ![]() ,
которая может быть найдено, если задана функция
,
которая может быть найдено, если задана функция ![]() ,
характеризующая действие источника энергии. В частных случаях, когда к цепи
подключаются источники постоянного и синусоидального напряжений, составляющую
,
характеризующая действие источника энергии. В частных случаях, когда к цепи
подключаются источники постоянного и синусоидального напряжений, составляющую ![]() определяют методами расчета для
установившегося режима.
определяют методами расчета для
установившегося режима.
Отыскание постоянных интегрирования Ак проводят, исходя из начальных условий.
Учитывая вышеизложенное, сформулируем АЛГОРИТМ РАСЧЕТА ПЕРЕХОДОВ ПРОЦЕССОВ в цепях классическим методом.
1. Для цепи, сформированной в результате коммутации,
составляют дифференциальное уравнение ![]() -го
порядка, в которое входит только одна искомая функция тока или напряжения. В
качестве такой функции выбирают ту, которая согласно законам коммутации,
скачком не изменяется.
-го
порядка, в которое входит только одна искомая функция тока или напряжения. В
качестве такой функции выбирают ту, которая согласно законам коммутации,
скачком не изменяется.
2. Записывают характеристическое уравнение и определяют его
корни:![]()
3. Определяют начальные условия в цепи: ![]() .
.
4. Определяют принужденную составляющую ![]() .
.
5. Искомую функцию записывают в общем виде как сумму ![]() , определяют ее
, определяют ее ![]() производные
производные ![]() и
путем решения полученной системы уравнений с учетом начальных условий,
определяют постоянные интегрирования
и
путем решения полученной системы уравнений с учетом начальных условий,
определяют постоянные интегрирования ![]() .
.
6. Записывают окончательное выражение искомой функции, определяют остальные функции тока или напряжения и строят графики их зависимости от времени.
По этому алгоритму проведем анализ переходных процессов в неразветвленных цепях первого и второго порядка.
2.3. Свободные процессы в цепях первого порядка. Длительность свободных процессов
2.3.1. Свободные процессы в ![]() -
цепи
-
цепи
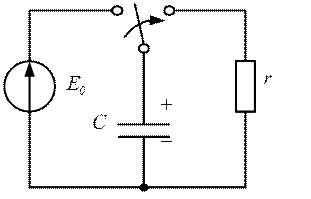
Рис. 2.5
Свободные процессы в ![]() -
цепи могут происходить при отсутствии в ней источников и ненулевых начальных
условиях. Качественный анализ процессов в схеме, приведенной на рисунке,
показывает, что до коммутации емкость С
была заряжена до напряжения, равного э.д.с. источника
-
цепи могут происходить при отсутствии в ней источников и ненулевых начальных
условиях. Качественный анализ процессов в схеме, приведенной на рисунке,
показывает, что до коммутации емкость С
была заряжена до напряжения, равного э.д.с. источника ![]() ,
токи во всех участках цепи отсутствовали. После коммутации емкость С разряжается через сопротивление
,
токи во всех участках цепи отсутствовали. После коммутации емкость С разряжается через сопротивление ![]() , напряжение на емкости будет
уменьшаться, а соответственно и на сопротивлении, разрядный ток будет
уменьшаться от величины
, напряжение на емкости будет
уменьшаться, а соответственно и на сопротивлении, разрядный ток будет
уменьшаться от величины
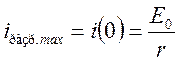 до нуля.
до нуля.
Из приведенного выражения видно, что разрядный ток будет тем меньше, чем больше r и наоборот. Длительность переходных процессов будет тем больше, чем больше r, а также чем больше C, т.к. большая емкость содержит больший заряд.
Найдем законы изменения напряжений ![]() ,
и ток
,
и ток ![]() путем точного анализа процессов по
сформулированному ранее алгоритму.
путем точного анализа процессов по
сформулированному ранее алгоритму.
1. Составление дифференциального уравнения.
Согласно II закону Кирхгофа для
цепи, сформулированной в результате коммутации, имеем ![]() .
В качестве исходной функции выберем
.
В качестве исходной функции выберем ![]() , т.к. в
результате коммутации именно напряжение на емкости скачком не изменяется
, т.к. в
результате коммутации именно напряжение на емкости скачком не изменяется
![]() ,
, 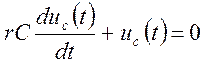 .
.
2. Запишем характеристическое уравнение ![]() ,
,
и найдем его корень 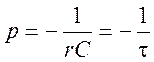 ,
где
,
где ![]() - постоянная времени цепи.
- постоянная времени цепи.
3. Определим начальное условие: - напряжения на емкости до коммутации равно величине э.д.с. источника
![]() .
.
4. Расчет принужденной составляющей: напряжение на емкости при
![]() уменьшится до нуля
уменьшится до нуля
![]() .
.
5. Запишем искомую функцию в общем виде как сумму
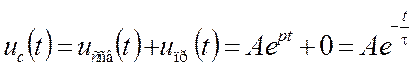 .
.
с учетом начальных условий, найдем постоянную интегрирования
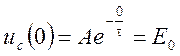 ;
; ![]() .
.
6. Окончательное выражение искомой функции имеет вид:
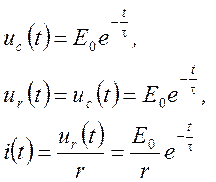 ,
,
или 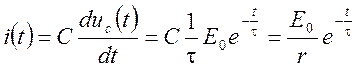 .
.
Графики ![]() ,
, ![]() приведены на рисунке 2.6. Значение
напряжения на емкости до коммутации равно
приведены на рисунке 2.6. Значение
напряжения на емкости до коммутации равно ![]() ,
а ток в цепи отсутствовал, что отражено на графике. На графике видно, что за
время, равное
,
а ток в цепи отсутствовал, что отражено на графике. На графике видно, что за
время, равное ![]() напряжение на емкости и
разрядный ток уменьшается в
напряжение на емкости и
разрядный ток уменьшается в ![]() раз, так как
раз, так как 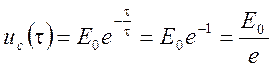 и
и 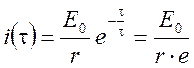
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.