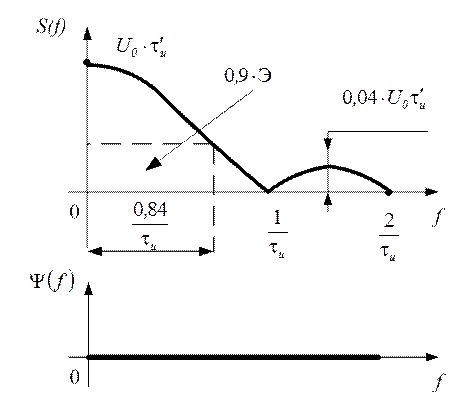
Рис. 1. 37
·
АЧС сплошной и изменяется по закону 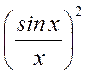 ,
максимальное значение АЧС при f=0
,
максимальное значение АЧС при f=0 ![]() .
.
·
Максимальное значение АЧС первого бокового лепестка равно ![]() тогда как у
одиночного прямоугольного видеоимпульса
тогда как у
одиночного прямоугольного видеоимпульса ![]() .
.
·
Ширина спектра на уровне 90% энергии сигнала равна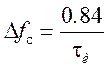 .
.
· ФЧС на всех частотах равен 0.
·
База сигнала, у которого длительность и ширина спектра определены
на уровне 90% его энергии, равна ![]() , т.е. сигнал является
простым.
, т.е. сигнал является
простым.
1.2.2 Одиночный радиосигналы и их спектры.
Одиночный прямоугольный радиоимпульс(ОПРИ)
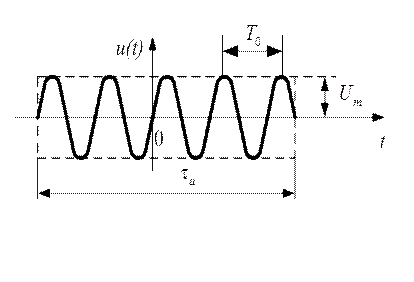
Рис. 1.38
ОПРИ (рис. 1.38) можно получить путем амплитудной модуляции высокочастотного колебания прямоугольным видеоимпульсом.
Аналитическое выражение ОПРИ:
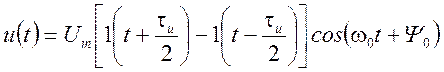
Спектральную плотность сигнала найдем путем вычисления интеграла
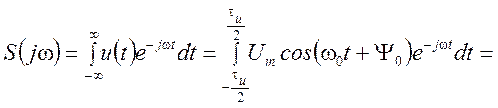
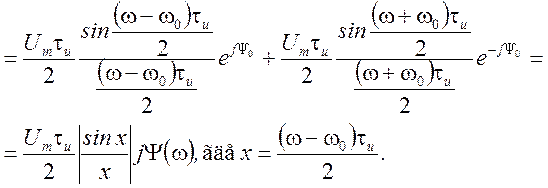
Отсюда 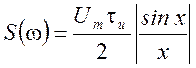 ,
,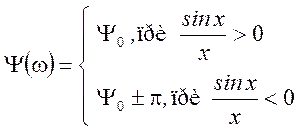
. 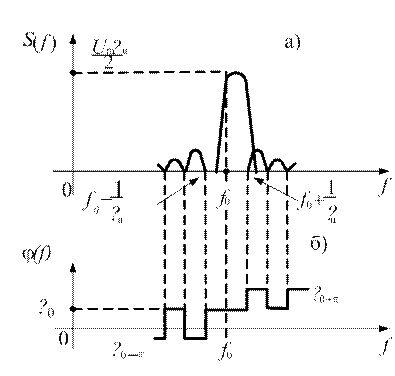
Рис. 1. 39
Из анализа графиков, приведенных на рисунке 1.39 следует:
· АЧС одиночного прямоугольного радиоимпульса сплошной, сосредоточен в окрестности несущей частоты.
·
Огибающая спектра изменяется по закону ![]() .
.
·
Максимальное значение АЧС при ![]()
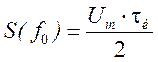 .
.
·
Ширина спектра на уровне 90% энергии сигнала 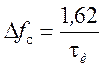 .
.
·
ФЧС в пределах нечетных лепестков равен ![]() ,
в пределах четных
,
в пределах четных![]() .
.
·
База сигнала ![]() ,
т.е. сигнал является простым. Если известен спектр модулирующей функции
,
т.е. сигнал является простым. Если известен спектр модулирующей функции ![]() ,то спектр радиосигнала формируется
следующим образом:
,то спектр радиосигнала формируется
следующим образом:
§ АЧС модулирующей функции смещается на частоту несущего колебания.
§ Максимальное значение модуля спектральной плотности (АЧС) уменьшается в два раза.
§ Сформированный таким образом спектр зеркально отображается относительно несущей частоты.
Одиночный колокольный радиоимпульс (ОКРИ)
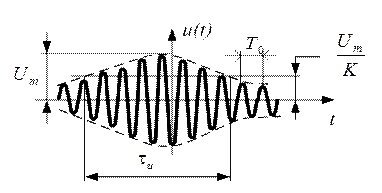
Рис. 1.40
ОКРИ (рис. 1.40) можно получить путем амплитудной модуляции высокочастотного колебания колокольнобразный видеоимпульсом.
Аналитическое выражение ОКРИ:
![]() ,
,
где 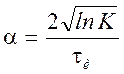 ,
при k=e
,
при k=e 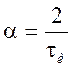 .
.
Спектральную плотность такого сигнала рисунок 1.41 рассчитывают путем вычисления интеграла Фурье.
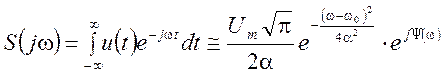 ;
;
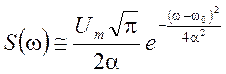 , при k=e,
, при k=e, 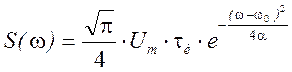 .
.
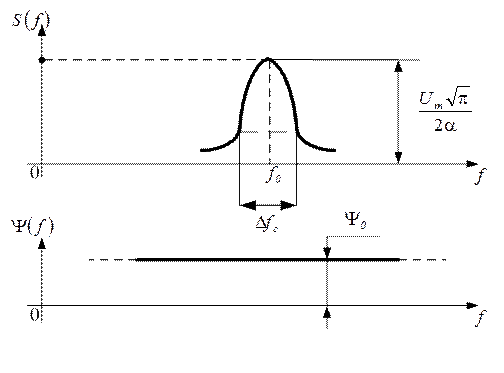
Рис. 1.41
Из анализа графиков приведенных на рисунке 1.41 следует:
· АЧС одиночного колокольного радиоимпульса сплошной и сосредоточен в окрестности несущей частоты.
· Огибающая АЧС имеет колокольную форму.
·
Максимальное значение АЧС при ![]() равно
равно
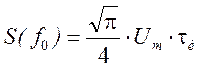
· Ширина спектра на уровне 90% энергии сигнала равна 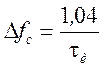 (k=e).
(k=e).
·
ФЧС во всем диапазоне частот
равен ![]() .
.
·
База сигнала при длительности импульса и ширине спектра сигнала
на уровне 90% его энергии ![]() ,
т.е. сигнал является простым.
,
т.е. сигнал является простым.
1.3. ПЕРИОДИЧЕСКИЕ СИГНАЛЫ И ИХ СПЕКТРЫ
Периодическая последовательность прямоугольных видеоимпульсов (ПППВИ).
Периодическая последовательность прямоугольных видеоимпульсов является модулирующей функцией для формирования периодической последовательности прямоугольных радиоимпульсов (ПППВИ), которые являются зондирующими сигналами для обнаружения и измерения координат движущихся целей. Поэтому, по спектру модулирующей функции (ПППВИ), можно относительно просто и быстро и определить спектр зондирующего сигнала (ПППРИ). При отражении зондирующего сигнала от движущейся цели изменяются частоты спектра гармоник несущего колебания (эффект Допплера). Вследствие чего, можно выделить полезный сигнал, отраженный от движущейся цели, на фоне мешающих (помеховых) колебаний, отраженных от неподвижных объектов (местные предметы) или малоподвижных объектов (метеообразования, стаи птиц и др.).
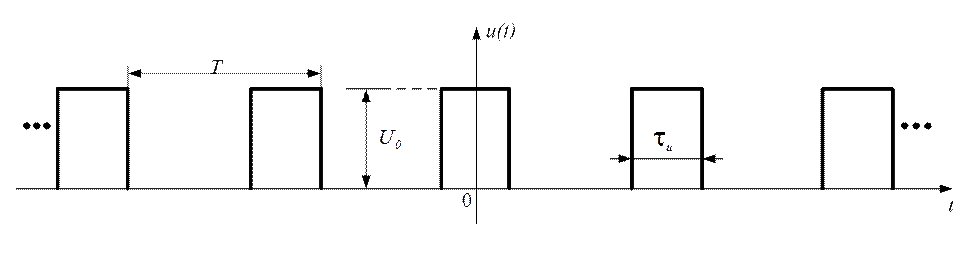
Рис. 1.42
ПППВИ (рис. 1.42) представляет собой совокупность одиночных прямоугольных видеоимпульсов, следующих друг за другом через равные промежутки времени. Аналитическое выражение сигнала.
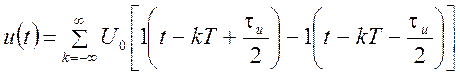 ,
,
где
![]() - амплитуда импульсов;
- амплитуда импульсов;
![]() - длительность импульсов;
- длительность импульсов;
![]() - период следования
импульсов;
- период следования
импульсов;
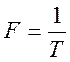 -.частота следования
импульсов,
-.частота следования
импульсов, ![]() ;
;
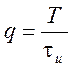 - скважность.
- скважность.
Для вычисления спектрального состава периодической последовательности импульсов применяют ряд Фурье. При известных спектрах одиночных импульсов, образующих периодическую последовательность, можно воспользоваться связью между спектральной плотностью импульсов и комплексными амплитудами ряда:
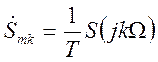 .
.
Для одиночного прямоугольного видеоимпульса спектральная плотность описывается формулой
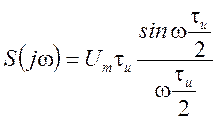 .
.
Воспользовавшись связью между спектральной плотностью одиночного импульса и комплексными амплитудами ряда, находим
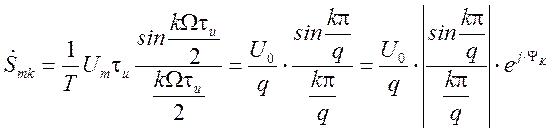 ,
,
где ![]() =
0; ± I; ± 2; ...
=
0; ± I; ± 2; ...
Амплитудно-частотный спектр (рис. 1.43) будет представлен совокупностью составляющих:
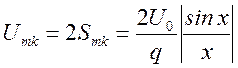 ,
,
при этом положительным значениям 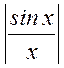 соответствуют
нулевые начальные фазы, а отрицательным - начальные фазы, равные
соответствуют
нулевые начальные фазы, а отрицательным - начальные фазы, равные ![]() .
.
Таким образом, аналитическое выражение ПППВИ будет равно
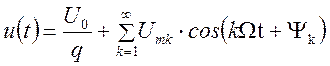 .
.
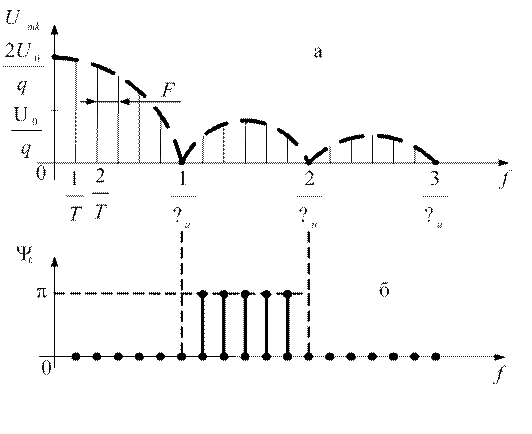
Рис. 1.43
Из анализа графиков, приведенных на рисунке 1.43 следует:
·
Спектр ПППВИ дискретный состоящий из отдельных гармоник с
частотой ![]() .
.
·
Огибающая АЧС изменяется по закону ![]() .
.
·
Максимальное значение огибающей при ![]() равно
равно
![]() , значение постоянной составляющей
, значение постоянной составляющей ![]() .
.
·
Начальные фазы гармоник в пределах нечетных лепестков равны 0, в
пределах четных ![]() .
.
·
Количество гармоник в пределах каждого лепестка равно ![]()
·
Ширина спектра сигнала на уровне 90% энергии сигнала 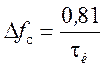
·
База сигнала ![]() ,
поэтому сигнал является простым.
,
поэтому сигнал является простым.
Если изменять длительность импульсов ![]() , либо частоту их повторения F (период
, либо частоту их повторения F (период ![]() ), то параметры спектра и его АЧС
будет изменяться.
), то параметры спектра и его АЧС
будет изменяться.
На рисунке 1.43 представлен пример изменения сигнала и его АЧС при увеличении длительности импульса в два раза.
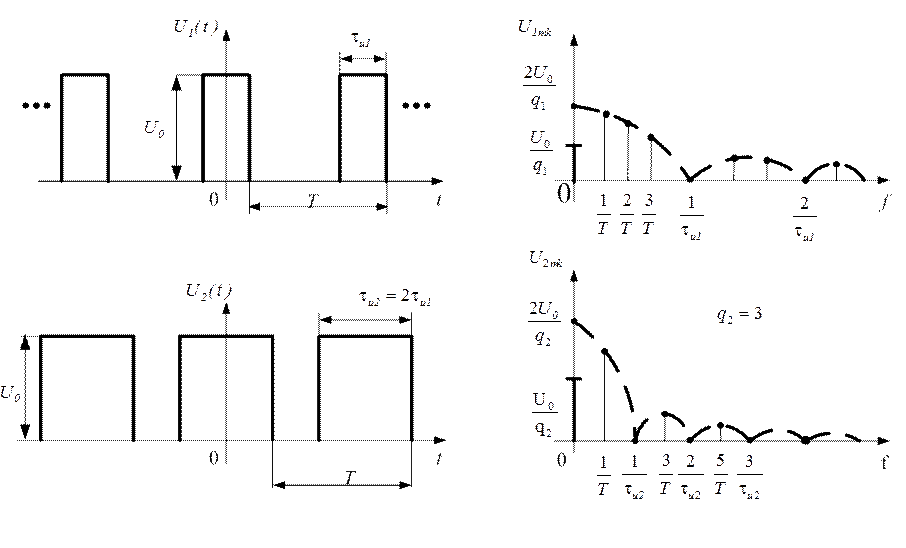
Рис. 1.44
Периодические последовательности прямоугольных
видеоимпульсов и их АЧС параметрами ![]() , T,.
, T,. ![]() и
и
![]() , T,
, T, ![]() изображены
на рисунке 1.44.
изображены
на рисунке 1.44.
Из анализа приведенных графиков следует:
1)
Для ПППВИ с длительностью импульса ![]() :
:
а) Скважность q=4, следовательно, в пределах каждого лепестка сосредоточено 3 гармоники;
b) Частота к-ой гармоники ![]() ;
;
с)
Ширина спектра сигнала на уровне 90% энергии ![]() ;
;
d) Постоянная составляющая равна ![]()
2)
Для ПППВИ с длительностью импульса ![]() :
:
а) Скважность q=2, следовательно, в пределах каждого лепестка находится 1 гармоника;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.