При подаче управляющего импульса, тиратрон открывается (замыкание электронного ключа), при этом вся накопленная энергия через импульсный трансформатор подается на нагрузку и накопительные ёмкости формирующей линии полностью разряжаются. Этот процесс происходит очень быстро (значительно быстрее, чем заряд). После разряда емкостей в цепи вновь имеют место нулевые начальные условия и процесс заряда повторяется вновь и вновь.
2.7.2. Применение цепи второго порядка в схеме "генератор с контуром ударного возбуждения (КУБ)
![]()
![]()
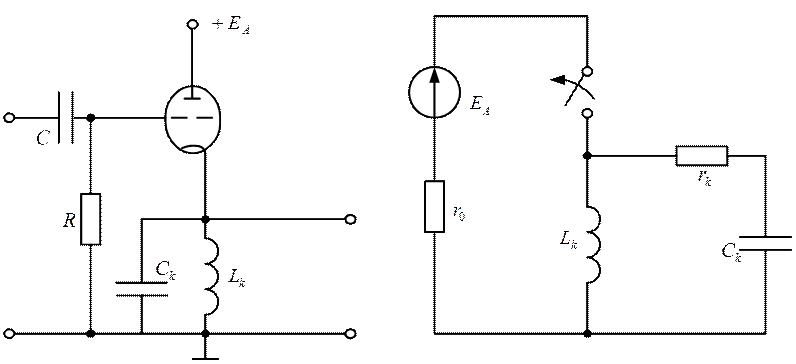
а) Принципиальная схема б) Эквивалентная схема
Рис. 2.31
В исходном состоянии лампа (может быть использован
транзистор) открыта. От " + " источника через лампу и индуктивность ![]() к " - " источника течет первоначальный ток, равный
к " - " источника течет первоначальный ток, равный 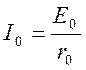 где
где ![]() - сопротивление лампы постоянному току.
- сопротивление лампы постоянному току.
При подаче на сетку лампы длительного отрицательного
(запирающего лампу) импульса, лампа прекращает проводить ток, это равнозначно
размыканию ключа на эквивалентной схеме (рис. 2.31). При этом запасенная в
индуктивности энергия, первоначальный запас которой равен 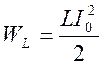 будет циркулировать в
будет циркулировать в ![]() - цепи в виде затухающих колебаний
тока и напряжения.
- цепи в виде затухающих колебаний
тока и напряжения.
Показанные на рисунке 2.32 колебания тока и напряжения находят широкое применение в РЭТ, в частности для создания спиральных разверток на специальных экранах, для формирования масштабных отметок дальности в выносных индикаторах РЛС и проч.

Рис. 2.32
2.7.3. Прохождение радиоимпульса прямоугольной формы через колебательный контур
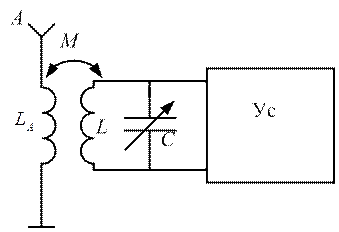
Рис. 2.33
Радиоприёмные устройства РЛС содержат в своем составе
колебательные контуры (рис. 2.33), настроенные на частоту зондирующего сигнала.
В качестве зондирующих сигналов в РЛС применяются радиоимпульсы прямоугольной
формы. Рассмотрим прохождение отраженного от цели прямоугольного радиоимпульса
через входную цепь приемного устройства. Под воздействием принятого сигнала в
катушке ![]() протекает ток, соответствующий по
форме отраженному сигналу. В результате явления взаимной индукции в катушке
протекает ток, соответствующий по
форме отраженному сигналу. В результате явления взаимной индукции в катушке ![]() наводится Э.Д.С. прямоугольной формы.
Под действием этой э.д.с. происходит процесс установления колебаний в контуре.
По отношению к наводимой э.д.с. все элементы контура включены последовательно,
поэтому контур является последовательным. В последовательном колебательном
контуре, резонансная частота которого совпадает с частотой сигнала, будет иметь
место процесс плавного нарастания амплитуды напряжения на емкости контура до
установившегося значения, равного
наводится Э.Д.С. прямоугольной формы.
Под действием этой э.д.с. происходит процесс установления колебаний в контуре.
По отношению к наводимой э.д.с. все элементы контура включены последовательно,
поэтому контур является последовательным. В последовательном колебательном
контуре, резонансная частота которого совпадает с частотой сигнала, будет иметь
место процесс плавного нарастания амплитуды напряжения на емкости контура до
установившегося значения, равного ![]() . После окончания
импульса будет иметь место затухание колебаний.
. После окончания
импульса будет иметь место затухание колебаний.
Если на входе приёмника будет действовать помеха аналогичной формы с частотой, отличающейся от частоты контура, то установление колебаний напряжения на емкости контура будет сопровождаться биениями.
Максимальное значение установившегося напряжения на
емкости будет меньше, чем ![]() , после окончания
, после окончания
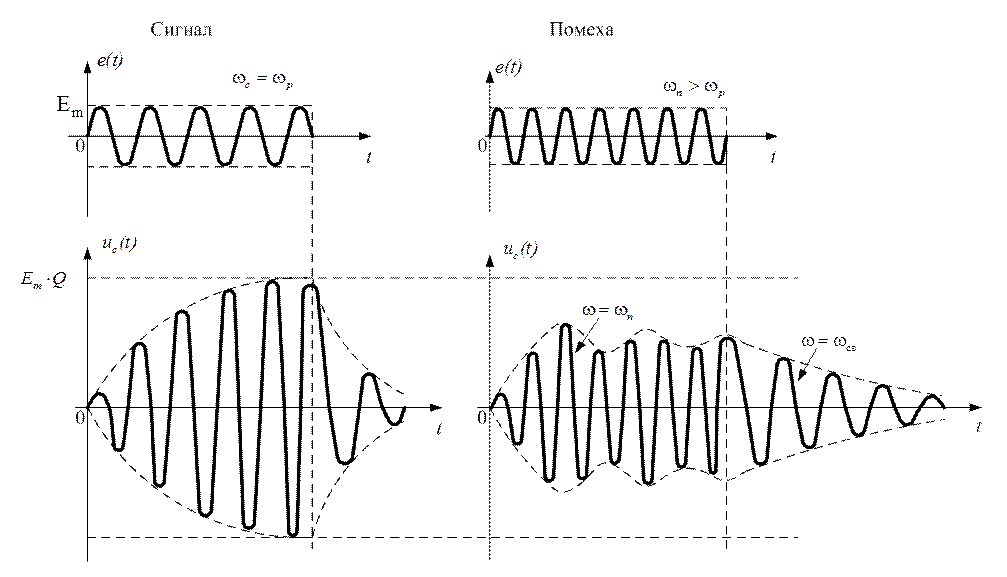
Рис.2.34
помехового импульса будет иметь место затухание колебаний с частотой, равной частоте свободных колебаний контура. Вышеизложенное иллюстрируется графиками.
Как видно из приведенных графиков, в любом случае имеет место изменение формы сигнала. Если полезный сигнал является достаточно "длинным", то переходными процессами в начале и в конце импульса можно пренебречь и полагать, что форма его не изменяется. Если полезный сигнал "короткий", то может случиться, что амплитуда колебаний не нарастет до своего максимального значения.
Степень изменения формы колебаний, как видно, обуславливается величиной добротности контура:
Максимальное значение ![]() также
зависит от добротности контура:
также
зависит от добротности контура:
![]()
где 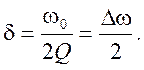
Максимальное значение ![]() также
зависит от добротности контура.
также
зависит от добротности контура.
Вывод: Выигрывая в избирательности контура при увеличении Q и в амплитуде установившихся колебаний, мы ухудшаем форму сигнала на емкости контура, и наоборот, стремясь обеспечить неискаженную передачу сигнала, мы должны уменьшить добротность контура, т.е. расширить полосу пропускания, что приводит к ухудшению избирательности контура.
2.8. Анализ переходных процессов в цепях без составления дифференциальных уравнений
2.8.1. Переходные процессы в разветвленных цепях
При анализе переходных процессов в разветвленных цепях при нулевых начальных условиях можно не составлять дифференциальное уравнение, а воспользоваться полученным ранее решением для неразветвленной цепи. Однако, предварительно следует заданную схему заменить эквивалентным генератором.
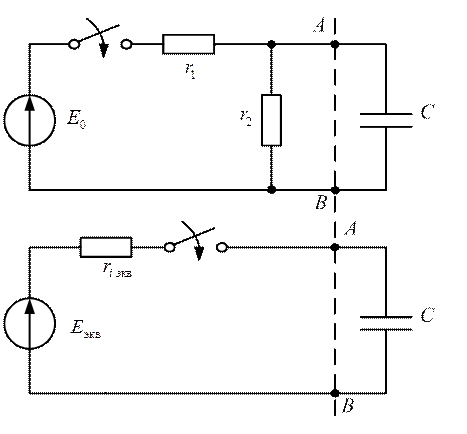
Рис. 2.35
Параметры эквивалентного генератора находятся следующим образом:
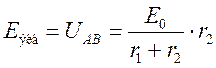
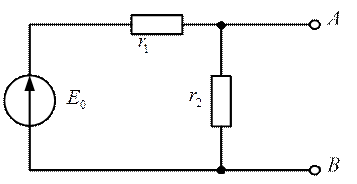
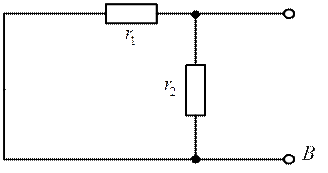
Рис. 2.36
т.к. Э.Д.С. эквивалентного генератора равно:
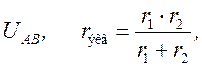
т.к.
сопротивление между зажимами АВ схемы без источника(рис. 2.36, нижняя) является
внутренним сопротивлением эквивалентного генератора. Учитывая Еэкв
и ri экв,
напряжение на емкости после коммутации 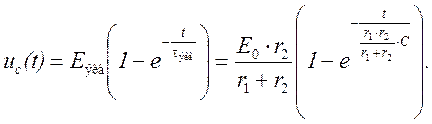
График изменения напряжения на емкости приведен на рис. 2.37
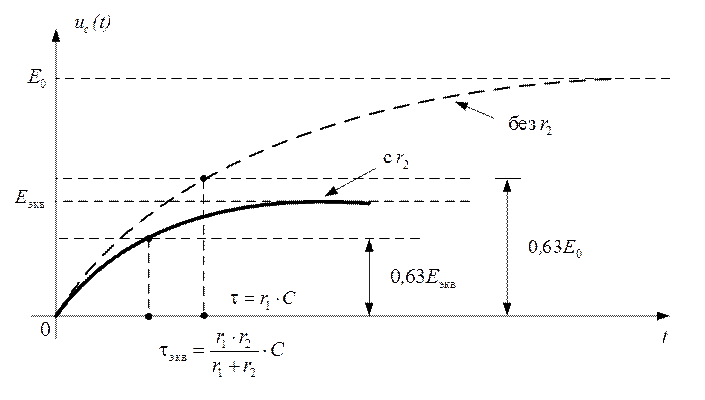
Рис. 2.37
Аналогичные процессы могут происходить и в схеме с индуктивностью (рис. 2.38). Изменение тока в индуктивности будет происходить согласно выражению:
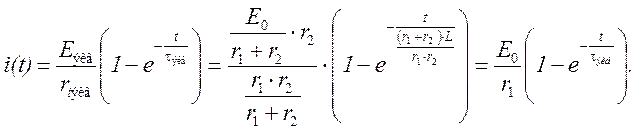
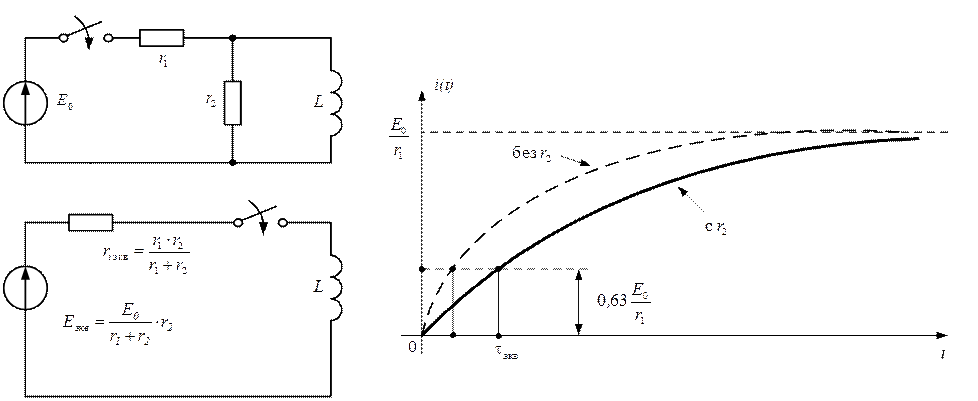
Рис. 2.38
1)Рассмотренные цепи отличаются от изученных ранее наличием сопротивления r2, что позволяет оценить влияние изменения схемы на переходные процессы.
2) В rC – цепи отличия таковы:
а) в цепи без r2 конденсатор заряжался до величины E0 с постоянной времени равной ![]()
б) в цепи с r2 конденсатор
заряжался до напряжения 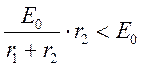 с постоянной
времени равной
с постоянной
времени равной 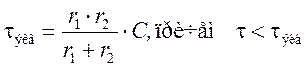 .
.
3) В rL - цепи отличия таковы:
а) в обоих случаях установившееся значение тока равно 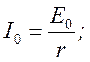
б) длительность переходного процесса будет больше т.к.
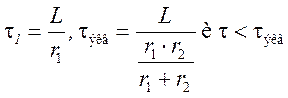 .
.
2.8.2 Качественный анализ свободных и переходных процессов в цепях первого и второго порядков
Качественный анализ свободных и переходных процессов в цепях первого и второго порядков состоит в следующем:
а) для цепей первого порядка:
определяют начальные условия, принужденную составляющую.
Исходя из анализа схемы определяют какой процесс в цепи будет иметь место после
коммутации, свободный или переходной 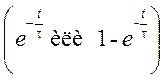 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.