2.Произвести оптимизацию следящей системы по
параметру![]()
![]() ,
используя критерий минимума среднего квадрата ошибки; определить
оптимальное значение шумовой полосы
,
используя критерий минимума среднего квадрата ошибки; определить
оптимальное значение шумовой полосы ![]() системы и
минимально допустимую ошибку слежения
системы и
минимально допустимую ошибку слежения ![]() ;
построить графики зависимостей результирующей средней квадратической ошибки
слежения, а также её составляющих (динамической и шумовой) от полосы.
;
построить графики зависимостей результирующей средней квадратической ошибки
слежения, а также её составляющих (динамической и шумовой) от полосы.
Оптимизация системы по критерию минимума
сводится к нахождению параметра![]() , при
котором обеспечивается минимум величины:
, при
котором обеспечивается минимум величины:
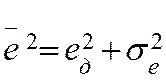 (1)
(1)
при заданной структуре системы (вид
передаточной системы ![]() ) и значения параметров
) и значения параметров ![]() ,
, ![]() .
По формуле (1) определяют средний квадрат ошибки слежения
.
По формуле (1) определяют средний квадрат ошибки слежения 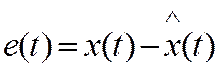 в установившемся режиме (
в установившемся режиме (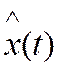 - оценка задающего воздействия).
Составляющая
- оценка задающего воздействия).
Составляющая ![]() определяет динамическую
ошибку, обусловленную инерционностью следящей системы по отношению к
меняющемуся задающему воздействию (при детерминированном воздействии ошибка
также детерминированная). Составляющая
определяет динамическую
ошибку, обусловленную инерционностью следящей системы по отношению к
меняющемуся задающему воздействию (при детерминированном воздействии ошибка
также детерминированная). Составляющая ![]() определяет
дисперсию шумовой ошибки
определяет
дисперсию шумовой ошибки 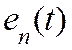 , обусловленной
помехой
, обусловленной
помехой ![]() . Таким образом, формула (1)
определяет средний квадрат результирующей ошибки
. Таким образом, формула (1)
определяет средний квадрат результирующей ошибки 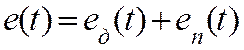 .
.
Динамическая ошибка ![]() определяется
параметром
определяется
параметром ![]() и
и ![]() задающего
воздействия, а также порядком астатизма (числом интеграторов), добротностью
задающего
воздействия, а также порядком астатизма (числом интеграторов), добротностью ![]() . Для системы первого порядка
установившиеся ошибка равна:
. Для системы первого порядка
установившиеся ошибка равна:
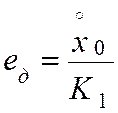 . (2)
. (2)
где K1,с-1 – добротность системы по скорости (k=1).
Вычисление шумовой полосы следящей системы упрощается, если подынтегральное выражение в виде:
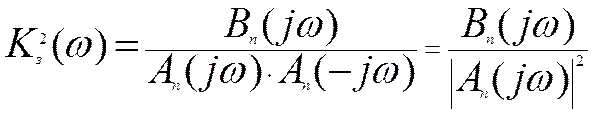 ,
,
Где полиномы An(jw) и Bn(w) определяются как:
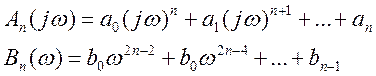 |
|||
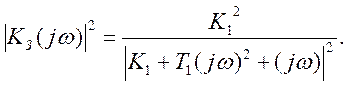
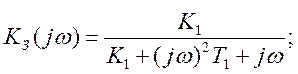 |
проанализировав данное выражение, приходим к соображениям что:
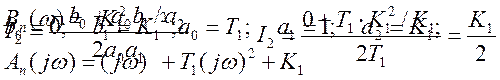 |
Для системы описываемой дифференциальными уравнениями второго порядка n=2, значения табличного интеграла будут выглядеть в виде:
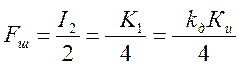 |
Найдем оптимальное значение шумовой полосы:
Отсюда дисперсия шумовой ошибки:
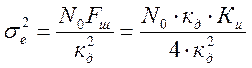 |
Найдём оптимальное значение параметра Кu, для этого продифференцируем выражение для среднего квадрата ошибки и приравняем производную к нулю:
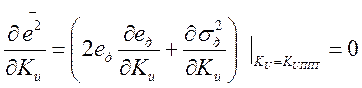
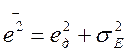
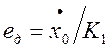
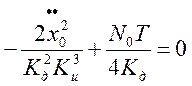
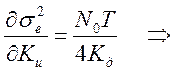
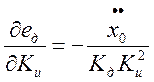 Где
Где
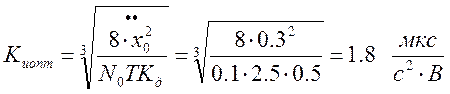 Из получившегося уравнения
найдем искомую величину Kuопт:
Из получившегося уравнения
найдем искомую величину Kuопт:
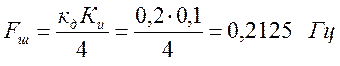 |
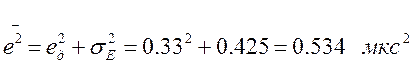
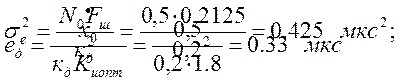 |
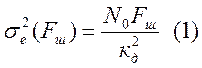 |
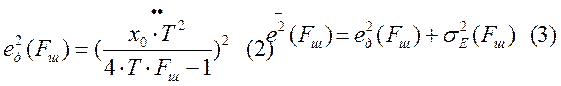 |
||
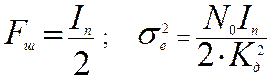 (7)
(7)
сводится к вычислению интеграла:
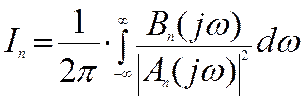 .
.
Значение, которого при ![]() определяется формулой:
определяется формулой:
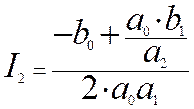 (8)
(8)
АЧХ замкнутой системы может быть найдена, следующим способом:
Заменим в передаточной характеристике
параметр ![]() на
на ![]() ,
тогда получим выражение для комплексного коэффициента передачи замкнутой
системы:
,
тогда получим выражение для комплексного коэффициента передачи замкнутой
системы:
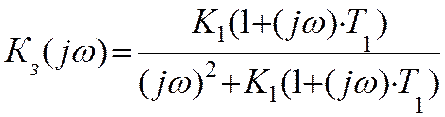
Тогда для квадрата модуля комплексного коэффициента передачи (квадрат АЧХ системы) запишем:
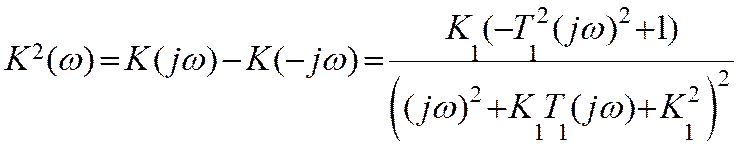
Откуда: ![]()
![]() .
.
Тогда в соответствии с формулой (6), для
коэффициентов полинома запишем ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]()
Подставив значения параметров в выражение (8) получим:
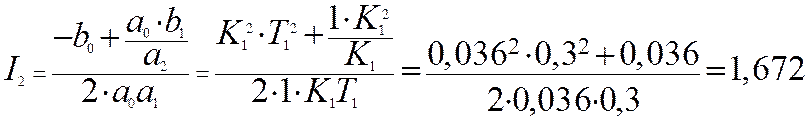
Используя (7) находим шумовую полосу системы и дисперсию шумовой ошибки:
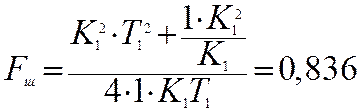 ;
; 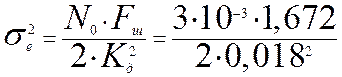
Далее определим средний квадрат результирующей ошибки:
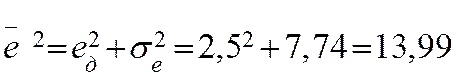
Произведем оптимизацию системы, учитывая, что порядок астатизма системы равен k=2.
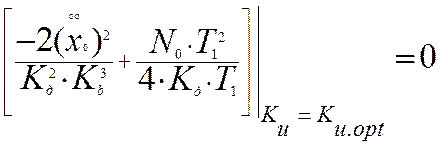
Решая это уравнение, получим:
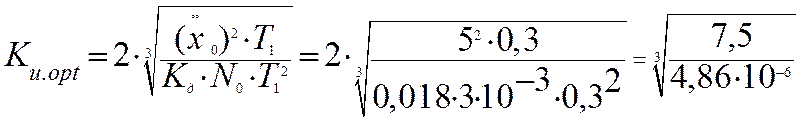
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.