Рассеяние Мандельштама-Бриллюэна. Дифракция в кристаллах. Поляризационные эффекты. Элементы статистической термодинамики. Излучение фотонов и эмиссия электронов

для волны

;                                        (10.5)

для волны

,                                               (10.6)

где q - угол наблюдения света.

Объединяя условия (10.5) и (10.6), получаем общее условие главных максимумов

.                                            (10.7)

Условие (10.7) аналогично условию главных максимумов для обычной дифракционной решетки с периодом d

.                                              (10.8)

§ 10.2. Рассеяние Мандельштама-Бриллюэна

Дифракция света может происходить не только на ультразвуковой волне, возбуждаемой в среде независимым генератором ультразвука, но и на собственных упругих колебаниях твердых тел и жидкостей. Такой вид дифракции носит название рассеяния Мандельштама-Бриллюэна.

Рассмотрим рассеяние света на неоднородностях среды, создаваемых тепловыми колебаниями плотности или упругими волнами (гиперзвуком). Колебания атомов среды можно представить как набор плоских звуковых волн широкого диапазона частот, распространяющихся во всевозможных направлениях. Суперпозиция звуковых волн вызывает появление флуктуации плотности и, следовательно, диэлектрической проницаемости и показателя преломления среды.

В кристаллах упругие волны одинаковой частоты, бегущие навстречу друг другу, образуют стоячие волны, т.е. создают периодическую структуру, на которой происходит дифракция света. Рассеяние света происходит по всем направлениям, но вследствие интерференции света за рассеяние в данном направлении ответственна звуковая волна определенной частоты.

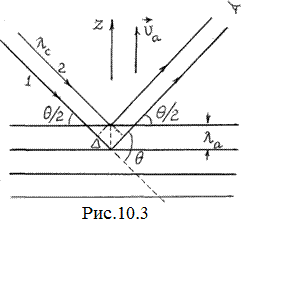
Рассмотрим дифракцию световой волны l_Cна периодической решетке с периодом, равным длине рассеивающей акустической волны l_a. На рис. 10.3:

q / 2 – угол скольжения светового луча; q  – угол рассеяния света. Оптическая разность хода лучей 1 и 2:

2=2l_a×sin(q / 2).                                                (10.9)

Если оптическая разность хода лучей равна длине световой волны в кристалле, то наблюдается главный максимум рассеянного света

2l_asin (q / 2) =l_с / n,                                            (10.10)

где п – усредненный показатель преломления кристалла. Преобразуем (10.10), заменив l_с=c/n_cи l_a=c/n_a,

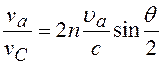,                                         (10.11)

где n_a, v_с, с, u_a, – соответственно частоты и скорости света и звуковой волны.

Из закона сохранения энергии следует: когда фотон передает энергию звуковой волне, возбуждая акустический квант энергии (фонон),

;                                       (10.12)

когда фотон поглощает фонон,

,                                       (10.13)

где hv¢_с – энергия фотона после рассеяния на фононе; hv_a – энергия фонона; h – постоянная Планка.

Относительное изменение частоты рассеянного света

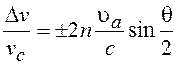.                                      (10.14)

В спектре рассеянного света появляются две дополнительные линии

,                                                (10.15)

Смещение  невелико, так как u_a<<с.

Для упругой волны, направленной вдоль оси zк наблюдателю, частота рассеянного света увеличивается вследствие эффекта Доплера (см. § 2.6), так как дифракционная решетка движется к наблюдателю, являясь источником вторичных гюйгенсовых волн. Для упругой волны, движущейся от наблюдателя,  < 0.

Поскольку упругая волна имеет одну продольную и две поперечные составляющие, имеющие одинаковую частоту и распространяющиеся с различными скоростями, рассеяние в кристалле приводит к появлению шести различных составляющих.

Заметим, что спектральные линии выше первого порядка имеют малую интенсивность и практически не наблюдаются.

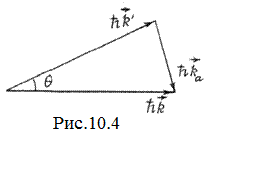
Квантово-механическое описание рассеяния света исходит из взаимодействия фотона с фононом. Запишем законы сохранения импульса и энергии для элементарного акта взаимодействия фотона с квантом звуковой волны (фононом) (рис. 10.4)

;                                            (10.16)

,                                          (10.17)

где k=2pn/l_C, k_a=2p/l_a ,w=2pn_с , w_a=2pn_a  – постоянная Дирака.

Из (10.16) следует ; . Учитывая, что k»k¢, имеем

,           (10.18)

Выразив k и k_aчерез l_с/n и l_a , получим выражение (10.10). Заменяя k_a=w_a/u_a, k=w×n/c, w_a=w – w¢, получаем (10.14).

Создание лазеров привело к открытию вынужденного Мандельштама-Бриллюэна рассеяния, обусловленного нелинейным взаимодействием возбуждающей световой волны и упругой тепловой или звуковой волны. Основой такого взаимодействия является эффект электрострикции, заключающийся в том, что диэлектрик в электрическом поле  меняет свой объем: таким образом, возникает электрострикционное давление, пропорциональное Е₂, и образуется упругая волна. В гигантском импульсе лазера при поле световой волны 10⁴ ¸ 10⁸ В/см электрострикционное давление достигает ~10⁵ атмосфер и возникает гиперзвук, частота которого составляет от 10⁹ до 10¹³ Гц. На частотах гиперзвука наблюдаются только нулевой и первый порядки дифрагированной световой волны. Поскольку упругие волновые фронты движутся со скоростью звука, частота дифрагированного света равна n+n_a, либо n – n_a.