ИСПОЛЬЗОВАНИЕ МЕТОДА ДИНАМИЧЕСКОГО РАССЕЯНИЯ СВЕТА ДЛЯ ОПРЕДЕЛЕНИЯ РАЗМЕРОВ ЧАСТИЦ КАК БЫСТРУЮ ПРОЦЕДУРУ ПРОВЕРКИ ОБРОЗЦОВ АНАЛИЗОВ МОЧИ
D. CHICEA, R. CHICEA, LIANA MARIA CHICEA
Аннотация. Эксперименты по динамическому рассеянию света были применены на моче человека. Результаты по измерению размеров частиц обсуждаются в контексте с выводами по стандартным лабораторным анализам мочи. Предлагается простая, но очень быстрая процедура проверки.
Ключевые слова: динамического рассеяние света, анализ мочи.
ВВЕДЕНИЕ
Когда когерентный пучок света имеет подвески как цель, каждая частица в свет рассеивается подвески. Когерентный всплески рассеянного каждой рассеивающего центра (СК) вмешиваться и в результате пятнистые дальнем поле. Список литературы [5] и [10] описывают явление. В работах [12, 13, 18, 19 20, 21] описывают несколько процедур в настоящее время используется для анализа спекл колебаний и [8] подарки в вводном разделе приводится краткий обзор методов анализа спекл. Наиболее изученных биологических частиц во взвешенном состоянии является красных кровяных клеток (эритроцитов).
В этой работе различные биологические жидкости был использован в качестве мишени для лазерного луча, а именно человеческая моча, как у здоровых и нездоровых людей. Различные частицы и клетки могут быть приостановлены в моче и выступать в качестве SC. Экспериментальная установка и краткое описание динамического рассеяния света техника (DLS), процедура обработки данных, и результаты представлены в следующих разделах.
МЕТОД ДИНАМИЧЕСКОГО РАССЕЯНИЯ СВЕТА (DLS)
DLS представляет собой хорошо отработанную методику измерения размеров частиц по размеру колеблются от нанометров до микрометров. Как уже говорилось ранее свет, рассеянный подвески представляет колебаний [5, 10]. Установив датчик под определенным углом и регистрации интенсивности рассеянного света временных рядов записывается. Как показано в [10, 22], ширина автокорреляционной функции временного ряда пропорциональна коэффициенту диффузии, которая, в свою очередь, зависит от того, гидродинамический диаметр частиц. Усовершенствованный вариант описан далее в этом разделе.
Переходя к деталям, наночастиц в водном растворе пройти трехмерное броуновское движение, которое является причиной наночастиц диффузии. Первые экспериментальные работы [9, 15] и дальнейшие теоретические трактаты [4, 11, 12], оказались в предположении, что спектр мощности интенсивность света, рассеянного частицами в суспензии может быть связано с функцией плотности вероятности (PDF). Эта связь между PDF и спектра мощности является следствием перевода относительного движения рассеивающих частиц в разности фаз рассеянного света. Таким образом, пространственные корреляции переведены на фазовых корреляций, которые проявляются в использовании теоремы Винера-Хинчина, касающиеся спектра мощности для автокорреляции процесса. Фазовых корреляций приводят к флуктуациям интенсивности рассеянного света, записанные с помощью детектора и системы сбора данных, в типичной экспериментальной установки, представленные на рис. 1.
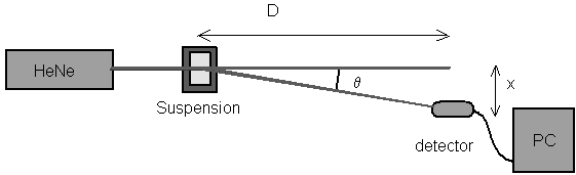
Рис.1. Типичная экспериментальная DLS установка.
Последовательность временных рядов записанных для образца u6-2 представлены на рис. 2. Путем вычитания из средней интенсивности записанных временных рядов и расчета площади интенсивности получим ряды времени. Преобразование Фурье временных рядов власть есть власть спектра. Мы можем сравнить спектр рассчитаны из экспериментальных данных с теоретически ожидаемым спектром, а именно функциональная форма линии лоренцевой S(f) (формула 1).
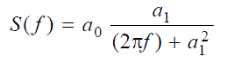 (1)
(1)
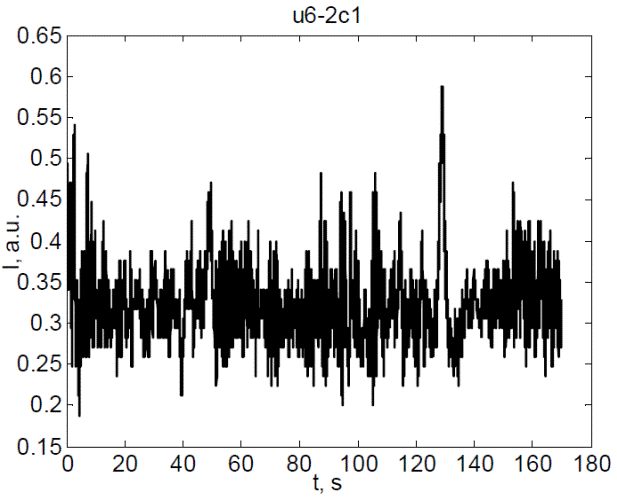
Рис. 2. Последовательность временных рядов записанных для образца u6-2.
(Суффикс с1 добавляется автоматически в соответствии с процедурой обработки данных).
Лоренцевой линии S(f) состоит из двух свободных параметров a0 и a1 и пригодно для использования спектра мощности нелинейного минимизация процедур, чтобы минимизировать расстояние между набора данных и линии. Заметим, что a0 входит линейно, поэтому он только выполняет масштабирование функции в диапазоне, что приводит к сдвигу в логарифмическом представлении. Параметр a1 входит нелинейно в функцию. Его действие в лог-журнала масштабного участка можно приблизительно описать как смещение по оси частот. Возможность установки все функции выгодным по сравнению с альтернативным методом, описанным в [5, 11, 15], где f1/2 (частота, где половину максимальной высоты достигается) была измерена, так как это занимает больше точек данных во внимание, что повышает качество подгонки.
После подгонки завершен, и параметры будут найдены, диаметр SCs можно оценить как двойное радиуса R. Радиус может быть получена как функция оборудованная параметр a1 и других известных величин по формуле (2):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.