Рассеяние Мандельштама-Бриллюэна. Дифракция в кристаллах. Поляризационные эффекты. Элементы статистической термодинамики. Излучение фотонов и эмиссия электронов, страница 13

3.  В каких случаях из распределений Ферми и Бозе – Эйнштейна можно получить распределения Больцмана?

4.  Чему равны площади, ограничиваемые графиками функций Максвелла на рис.13.4, 13.5, 13.6?

5.  Почему с увеличением температуры уменьшается вероятность того, что молекула может получить наиболее вероятную скорость?

ГЛАВА 14

излучение фотонов и эмиссия электронов

§ 14.1. Плотность энергии излучения и спектральная светимость

абсолютно черного тела

Пусть в твердом теле (термостате) имеется эвакуированная полость прямоугольной формы единичного объема ( = 1) с абсолютно черными стенками. В состоянии теплового равновесия стенки полости излучают и поглощают одинаковую энергию. Если бы энергия излучалась только параллельным пучком в направлении нормали к стенке полости, то плотность потока энергии была бы равна произведению плотности – энергии излучения на скорость света. Однако через каждую точку полости проходит множество фотонов, направления которых равномерно распределены в пределах телесного угла 4p. Тогда плотность потока энергии в произвольной точке полости в пределах телесного угла dW

                                                  (14.1)

где u – плотность энергии излучения частотой w; с – скорость света.

Рассмотрим на поверхности стенки полости площадку  (рис. 14.1). Поток энергии, излучаемой с поверхности площадки  в направлении нормали  к площадке, максимален, а в направлении под углом q = p/2 равен нулю. Поток энергии излучаемой с поверхности площадки  в пределах телесного угла dW в направлениях, образующих с нормалью n угол q.

,                                   (14.2)

где dW =2p×sinqdq,                                              

Поток энергии по всем направлениям в пределах телесного угла 2p

с поверхности

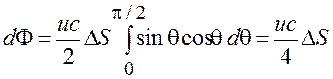                                 (14.3)

Энергия излучения частотой w, испускаемого с единицы поверхности в единицу времени, называется спектральной светимостью

                                           (14.4)

§ 14.2. Функция Планка

Функция, выражающая зависимость плотности энергии излучения либо спектральной светимости абсолютно черного тела от частоты излучения, называется функцией Планка.

Средняя энергия для каждого состояния равна произведению энергии кванта излучения  на вероятность заполнения состояния, определяемую функцией Бозе-Эйнштейна (см. § 13.3). Плотность излучения равна произведению плотности состояний с частотой со на среднюю энергию, приходящуюся на каждое состояние:

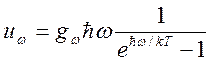,                                          (14.5)

где g_w – число состояний в единице объема (плотность состояний).

В случае теплового равновесия между излучением и веществом химический потенциал для фотонов равен нулю, поэтому в (14.5) Е=m заменяем энергией фотона Е =.

Определим  плотность состояний g_w=dN/dw. Найдем сначала dN = g_wdw. Для этого выберем шаровой слой в пространстве импульсов фотонов 4pp²dp (рис.14.2).  Элементарная  ячейка пространства импульсов равна  h³ [см. (19.48)].

Плотность состояний для фотонов, импульсы которых заканчиваются в пределах шарового слоя «толщиной» dp

.                                                  (14.6)

Заменив р = , получим выражение для плотности состояний с фиксированной частотой

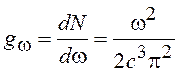.                                                         (14.7)

Учитывая две взаимно перпендикулярные поляризации для каждого из фотонов, запишем окончательно

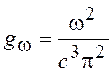.                                                                     (14.8)

Подставив (14.8) в (14.5), получим функцию Планка для плотности излучения

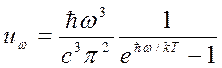.                                         (14.9)

Функция Планка для спектральной светимости абсолютно черного тела У учетом (14.4)

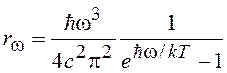.                                        (14.10)

Интегральная светимость абсолютно черного тела (Закон Стефана-Больцмана)

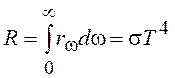,                                                (14.11)

где s= 5,67×10^-8 Вт/м²К⁴ – постоянная Стефана-Больцмана.

Заменив w = 2pс/l, в (14.10), получим зависимость спектральной светимости от длины волны излучения