Рассеяние Мандельштама-Бриллюэна. Дифракция в кристаллах. Поляризационные эффекты. Элементы статистической термодинамики. Излучение фотонов и эмиссия электронов, страница 8

В равновесном состоянии температуры систем равны. Из (12.15), (12.16) и (12.12) следует, что при диффузионном контакте двух систем в равновесном состоянии выравниваются частные производные от энтропии по числу частиц:

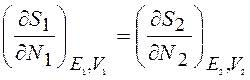                                     (12.17)

Чтобы обсудить это равенство, рассмотрим два способа изменения энергии системы. При тепловом контакте изменение энергии системы равно количеству тепловой энергии, передаваемой системе при обратимом равновесном процессе:

dE=dQ=TdS                                                          (12.18)

В случае диффузионного контакта изменение энергии системы происходит при диффузии частиц. Работа, совершаемая над системой в результате диффузии, называется химической работой. Тогда увеличение энергии системы

dE=dA=mdN                   (12.19)

Коэффициент m, называется химическим потенциалом и равен работе при диффузии одной частицы. Изменение энергии при тепловом и диффузионном контактах

dE=TdS+mdN.                                              (12.20)

Изменение энтропии системы

.                                      (12.21 )

Сравнив (12.21) и (12.16), видим, что

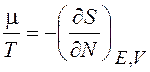                                          (12.22)

Из (12.22) видно, что в состоянии равновесия равны не только температуры, но и химические потенциалы двух систем, находящихся в диффузионном контакте:

m₁=m₂                                                 (12.23)

Если сначала T₁ = T₂ и m₁>m₂, то частицы будут перемещаться из системы 1 в систему 2. Покажем это. Учитывая, что dN₁=-dN₂и dE₁=-dE₂, запишем изменение энтропии

                       (12.24)

Поскольку система стремится к равновесному состоянию, энтропия системы возрастает и при m₁>m₂. Значит, частицы перемещаются из системы 1 с высоким значением химического потенциала в систему 2 с низким его значением. Системы с большей концентрацией частиц имеют больший химический потенциал, чем системы с низкой их концентрацией. Поэтому частицы стремятся диффундировать из областей с высокой концентрацией в области с низкой концентрацией.

Химический потенциал служит мерой зависимости числа доступных состояний от числа частиц в системе.

§ 12.4 "Механический" контакт двух систем.

Уравнение состояние идеального газа

Рассмотрим "механический" контакт двух систем, состоящих атомов идеального газа. Системы разделены поршнем, способным перемещаться без трения (рис. 12.3). В равновесном состоянии энтропия изолированной системы максимальна, поэтому выполняются соотношения

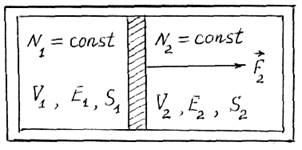dS₁= – dS₂ .(12.25)

Если результирующая сила переметает поршень на dx, то изменение энергии системы 2

dE¢₂=F₂dx=-P₂dV₂ ,                           (12.26)

	Рис. 12.3

 

где Р₂ – давление идеального газа в системе 2.

Знак "минус" учитывает уменьшение объема dV₂<0. Изменение энтропии системы зависит не только от энергии, но и от объема системы

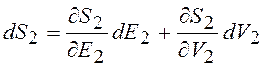.                                            (12.27)

Изменение энергии системы в этом случае

.                                 (12.28)

Отсюда

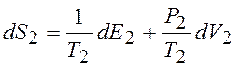.                                      (12.29)

Из сравнения (12.29) с (12.27) следует

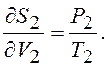                                                    (12.30)

Из (12.25) следует, что в равновсном состоянии выравниваются не только температуры, но и частные производные от энтропии по объёму, а следовательно и давление идеального газа в системах

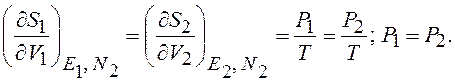                       (12.31)

Из соотношения (12.30) легко получить уравнение состояния идельного газа. Для этого необходимо определить производную ¶S/¶V при N=const. Представим энтропию системы в виде суммы

S = S_u = k lnW_u(12.33)

Пространственная составляющая статвеса для Nчастиц идеального газа, распределенных по ячейкам

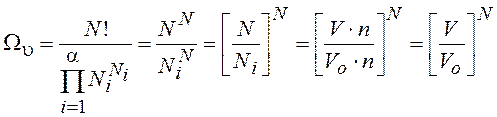,               (12.35)

где V₀ – объём ячейки; n – концентрация частиц.

Подставим (12.35) в (12.33):

S = kN ln V – kn ln V₀                                   (12.36)