Рассеяние Мандельштама-Бриллюэна. Дифракция в кристаллах. Поляризационные эффекты. Элементы статистической термодинамики. Излучение фотонов и эмиссия электронов, страница 7

W=ПW_I                                                        (12.1)

Соответственно энтропия системы, находящейся в равновесном состоянии,

                                                     (12.2)

§ 12.2. Тепловой контакт двух систем. Определение энтропии и температуры

Рис. 12.1

Рассмотрим изолированную систему, состоящую, в свою очередь, из двух систем, разделенных перегородкой с высокой теплопроводностью. Системы могут обмениваться только энергией, т.е. находиться в тепловом контакте (рис.12.1).

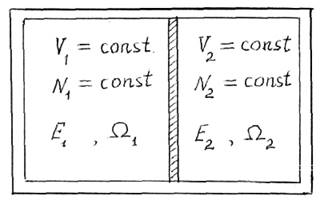
Рис. 12.1

Изолированной системой  называется система с постоянной энергией, постоянным числом частиц, находящихся в постоянном объеме;

E=E₁+E₂=const    N=N₁+N₂=const V=V₁+V₂=const(12.3)

Статвес равновесной системы

W=W₁+W₂                                                             (12.4)

Частицы, ударяясь о перегородку, передают энергию из одной системы в другую. Изменения энергий систем равны и противоположны по знаку

dE₁=-dE₂                                                                (12.5)

В равновесном состоянии статвес системы максимален. Тогда

W₁dW₂+W₂dW₁=0                                                  (12.6)

Разделим (12.6) на W₁W₂

dW₁/W₁ = -dW₂/W₂; dlnW₁=-dlnW₂                                               (12.7)

Из (12.7) видно, что относительное изменение статвеса, равное изменению логарифма статвеса, однозначно характеризует изменение состояния системы, поэтому lnW можно выбрать в качестве аддитивной функции состояния системы, не зависящей от предыстории состояния системы:

S = lnW.                                                       (12.8)

Энтропия служит мерой беспорядка в системе. Для изолированной равновесной системы энтропия максимальна. Тогда изменение энтропии равно нулю

dS=dS₁+dS₂=0; dS₁=-dS₂.                                              (12.9)

Поскольку при тепловом контакте энтропия зависит от энергии, преобразуем (12.9) следующим образом:

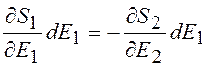                                  (12.11)

Заменим dE₂= – dE₁:

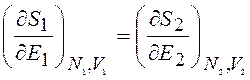                           (12.11)

Из (12.11) видно, что в состоянии равновесия систем при тепловом контакте двух систем выравниваются производные от энтропии по энергии при постоянном объеме и неизменном числе частиц каждой из систем. Эти производные можно выбрать в качестве интенсивного параметра, характеризующего равновесие системы. Величина, обратная частной производной от энтропии по энергии, называется температурой системы

                                          (12.12)

При таком определении температура измеряется в джоулях либо в электровольтах (1 эВ = 1,6×10^-19 Дж).

Отношение температуры в джоулях к температуре в градусах по шкале Кельвина k = 1.38×10^-23 Дж/К и называется постоянной Больцмана. Перейдем от безразмерной энтропии(12.8) к размерной

S º k lnW                                                      (12.13)

Тогда температура, определяемая (12.12), выразится в градусах Кельвина, или просто в Кельвинах. В состоянии равновесия температуры двух систем выравниваются:

T₁=T₂.                                                          (12.14)

Температура является интенсивным параметром системы, не зависящим от объема, энергии и числа частиц, заключенных в ней.

§ 12.3. Диффузионный контакт двух систем.

Определение химического потенциала

Рис. 12.2

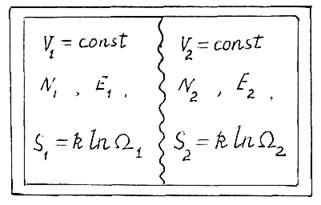Рассмотрим изолированную систему N частиц, состоящую, в свою очередь, из двух систем, разделенных пористой перегородкой, диффузионный контакт происходит при переходе атомов через перегородку. При этом системы обмениваются частицами и энергией  (рис.12.2). В равновесной системе энтропия максимальна и выполняются следующие соотношения:

dS₁= – dS₂; dN₁= – dN₂; dE₁= – dE₂;                              (12.15)

Энтропия системы является функцией энергии и числа частиц при постоянном объеме. Тогда изменения энтропии систем

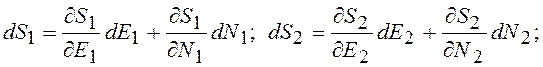          (12.16)