Рассеяние Мандельштама-Бриллюэна. Дифракция в кристаллах. Поляризационные эффекты. Элементы статистической термодинамики. Излучение фотонов и эмиссия электронов, страница 20

H₁₂ = H₂₁ » DE.                                             (15.49)

Запишем уравнения Шредингера в матричной форме

•

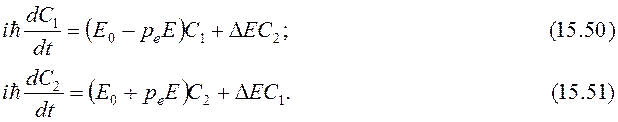Ищем решение в виде

                                                          (15.52)

                                                         (15.53)

где Е – неизвестная величина.

Подставляя эти решения в уравнения Шредингера и сокращая на экспоненту, имеем два соотношения

A₁ – (E – E₀ + p_eE) = DEA₂                                     (15.54)

A₁DE = (E – E₀ + p_eE) – A₂                                    (15.55)

Разделив одно уравнение на другое, решаем уравнение относительно E – E₀:

                                       (15.56)

В молекулярном квантовом генераторе p_eE << DE. Тогда, разлагая (15.56) в ряд и ограничиваясь двумя членами разложения, получаем

                                (15.57)

                                (15.58)

Соотношения (15.57) и (15.58) характеризуют квадратичный эффект Штарка.

При пропускании пучка молекул сквозь неоднородное электрическое поле квадрупольного конденсатора (рис.15.3,б) происходит сортировка молекул. Молекулы с повышенной энергией Е₂ имеют противоположно направленные векторы и , отклоняются к оси пучка в область слабого электрического поля и накапливаются в объёмном резонаторе. Молекулы с меньшей энергией E₁ удаляются из пучка.

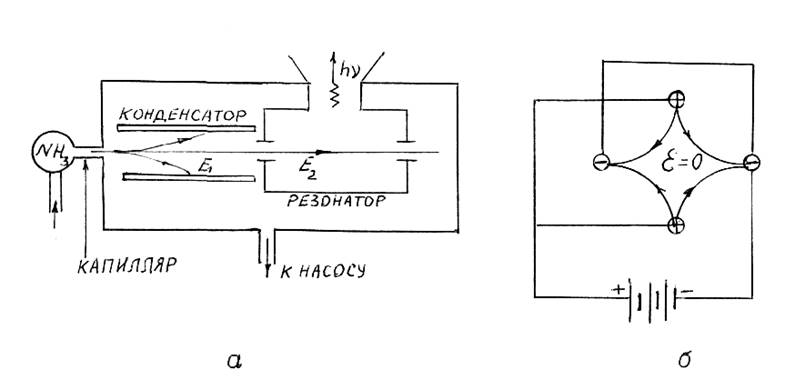
Рис. 15.3

Молекулы с энергией E₂ в резонаторе переходят в состояние с энергией E₁  излучают квант энергии hn= E₂ – E₁. После многократного отражения фотонов от стенок резонатора увеличивается время взаимодействия фотонов с возбужденными молекулами, которые вынужденно испускают такие же фотоны, так как в резонаторе выполняется условие инверсии населенностей N₂>N₁. Вынужденное излучение имеет такую же частоту, поляризацию и направление с вынуждающими переходы молекул фотонами. Кроме того, излучение является когерентным и характеризуется малым углом расходимости.

Интенсивность потока фотонов нарастает по экспоненциальному закону

,                                                (15.59)

где a – коэффициент квантового усиления; r - расстояние, пройденное фотонами в резонаторе; b – коэффициент поглощения, характеризующий потери энергии излучения в веществе.

Чем больше время Dt взаимодействия фотона с молекулами в резонаторе, тем меньше неопределенность частоты излучения, меньше ширина спектральной линии Dtn. Это следует из соотношения неопределенностей Гейзенберга hDnDt» h. Отсюда Dn»Dt^–1. Хаотичность теплового движения приводит к уширению спектральной линии, обусловленному эффектом Доплера. Для уменьшения эффекта Доплера пучок молекул направлен перпендикулярно выходу излучения (рис.15.3,а). Тогда проявляется лишь поперечный эффект Доплера, вызывающий меньшее изменение частоты, чем продольный (см. § 2.6). Относительная погрешность частоты Dn/n для квантовых генераторов на молекулах аммиака ~10^-11. Частота излучения 24870 МГц. Мощность излучения ~10^-10 Вт.

Меньшую погрешность можно получить в водородном квантовом генераторе (Dn/n = 3^.10^-12), в котором атомы водорода, имеющие магнитный момент , сортируются в неоднородном магнитном поле , создаваемом многополюсными магнитами. Атомы водорода, имеющие повышенное значение энергии при , антипараллельном полю , выталкиваются в область слабого магнитного поля и попадают в резонатор, имея энергию p_mB. В резонаторе выполняется условие инверсной населенности и происходит вынужденное излучение.

§ 15.4. Мощный газоразрядный лазер на смеси СO₂ и N₂