Рассеяние Мандельштама-Бриллюэна. Дифракция в кристаллах. Поляризационные эффекты. Элементы статистической термодинамики. Излучение фотонов и эмиссия электронов, страница 15

, где j – потенциал выхода; Е_F - энергия Ферми; Е_с – дно зоны проводимости полупроводника; DЕ_о – ширина запрещенной зоны; E_u –  потолок валентной зоны. Электрону, имевшему первоначально энергию Е при нулевой температуре Т = 0 К., при нагревании эмиттера должна быть сообщена дополнительная энергия для того, чтобы он покинул эмиттер.

Определим зависимость плотности тока термоэлектронной эмиссии из вырожденного полупроводникового термокатода (эмиттера) от его температуры Т. При Т = 0 К состояния с энергией Е < Е_F полностью заполнены электронами. Вероятность заполнения состояний при Т > 0 К определяется функцией Ферми

                               (14.18)

Потенциал выхода j обычно составляет > 1 В поэтому Е> Е_F и единицей в (14.18) можно пренебречь.

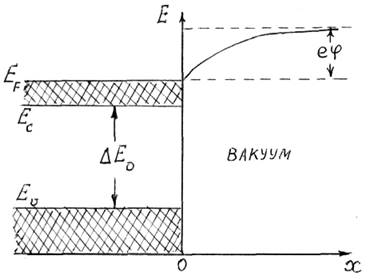
Рис. 14.4

Найдем число квантовых состояний в единице объема для значений импульсов электронов, лежащих в пределах от р_х до p_x + dp_x, от р_y до р_y + dp_y , от рz до р_z + dp_z. Элементарная ячейка пространства импульсов [см. формулу (16.10)]

Dp_xDp_yDp_z=h³                                                        (14.19)

В элементарной ячейке h³ имеется два доступных квантовых состояния, в которых в соответствии с принципом Паули может находиться не более двух электронов. Число состояний в дифференциальном объеме пространства импульсов

dN=2dp_xdp_ydp_z / h³(14.20)

соответствующее число электронов в этих состояниях

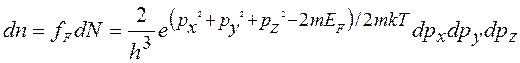, где р_x ³ 2m(E_F+ej).

Дифференциал плотности тока эмиссии

.                                            (14.22)

Плотность тока эмиссии

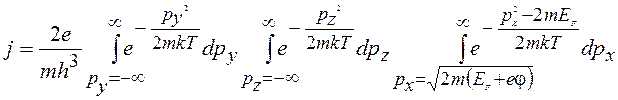               (14.23)

Первые два интеграла – табличные, вида

.

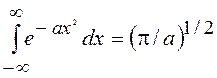Каждый из двух первых интегралов равен (2pmkT)^1/2. Третий интеграл найдем, заменяя показатель экспоненты новой переменной:

a = (p_x² – 2mE_F)/2mkT.

Тогда p_xdp_x=mkTda и нижний предел интегрирования а_o = еj/kТ. Третий интеграл

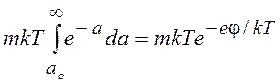,                                         (14.24)

Подставляя значения интегралов в (14.23), получаем закон Ричардсона-Дэшмана

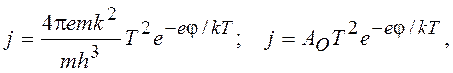                       (14.25)

где А₀ = 120,4 А/с²К².

Зависимость плотности тока эмиссии (14.25) получена в предположении, что поверхность эмиттера однородна и электронный газ в нем находится в состоянии термодинамического равновесия. В действительности равновесие нарушается отбором тока и проникновением внешнего электрического поля в эмиттер, а также зависимостью потенциала выхода от температуры. Учет указанных факторов приводит к значениям A_о от 15 до 350 А/см²К² для большинства чистых металлов.

§ 14.5.Эффект Шоттки

Определим уменьшение потенциала выхода j, обусловленное действием электрического поля E на эмиттер. Для этого сначала найдем силу, действующую на эмитированный электрон при E = 0.

Пусть эмитированный электрон находится на некотором расстоянии х от плоской безграничной поверхности металла (рис. 14.5).

Из закона сохранения заряда следует, что в металле индуцируется заряд, равный +е, так как до выхода электрона металл был электронейтральным. Поверхность металла является эквипотенциальной, и все силовые линии (рис. 14.5,а) должны подходить к поверхности

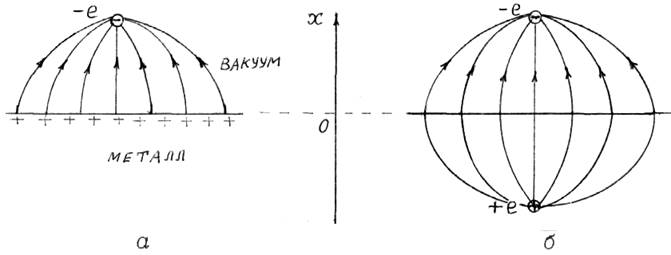
Рис. 14.5

металла под прямым углом. Для определения силы, действующей на электрон, применим метод изображений. Электрическое поле при х > 0 на рис. 14.9,а,б одинаково. Это значит, что сила, действующая на электрон на расстоянии х от поверхности металла, равна силе взаимодействия электрона с его „изображением” +е, находящимся на расстоянии – х,

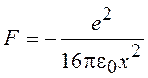                                            (14.26)

Потенциальная энергия электрона

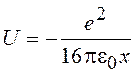                                              (14.27)

При х ® ¥ U=0 и величина потенциального барьера равна еj (рис.14.6,а). При действии ускоряющего поля E потенциальная энергия электрона изменяется на –еEx:

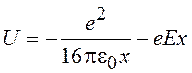.                                    (14.28)

Величина потенциального барьера уменьшается на еDj. Для вычисления уменьшения потенциала выхода Dj определим х_m, при котором потенциальная энергия (14.28) имеет максимум (рис.14.6,б)

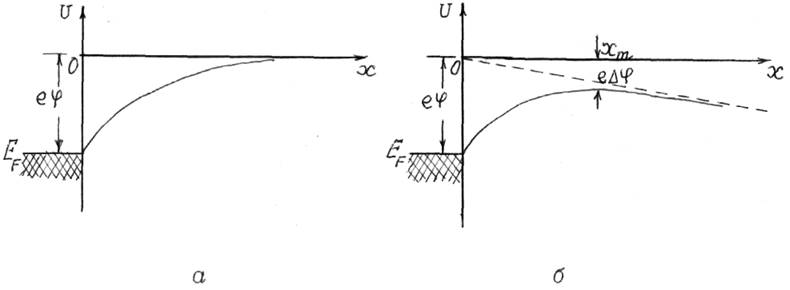
Рис. 14.6