Следует
заметить, что квантование орбитального движения электронов и образование
уровней Ландау происходит эффективно, когда период обращения электронов меньше
времени свободного движения электронов, а магнитное поле ![]() перпендикулярно
двумерному слою. Условия квантования орбитального движения можно выразить
соотношениями
перпендикулярно
двумерному слою. Условия квантования орбитального движения можно выразить
соотношениями
![]() (16.55)
(16.55)
Для
увеличения времени релаксации t и подвижности электронов
(образец необходимо охладить до гелиевых температур ~4O K)
а для увеличения циклотронной частоты обращения электронов wC
не
обходимо создать сильное магнитное поле ![]() .
.
1. Показать, что при образовании молекулы водорода происходит расщепление уровня энергии основного состояния электрона и между атомами создается ковалентная связь.
2. Объяснить образование энергетических зон в кристалле.
3. Во сколько раз изменится энергия Ферми в электронном невырожденном полупроводнике, если концентрацию доноров увеличить в 100 раз? Энергию ионизации доноров считать неизменной.
4. Как изменяется область насыщения при увеличении концентрации легирующей примеси в полупроводнике?
5. Почему при нагревании примесного полупроводника электропроводность в области насыщения уменьшается?
6.
В переходной области полупроводниковой структуры происходит искривление
энергетических зон и образуется двумерный вырожденный слой. Помещая такую
структуру в жидкий гелий и воздействуя
медленно изменяющимся магнитным полем B,
направленным перпендикулярно слою, квантуют энергию орбитального движения
электрона. Когда энергия уровня Ландау равна энергии Ферми, наблюдают
осцилляции
отраженного лазерного либо СВЧ–излучения от исследуемого слоя. Определить
концентрацию электронов в двумерном слое полупроводника, если период осцилляции
![]()
ГЛАВА 17
ФИЗИЧЕСКИЕ ЯВЛЕНИЯ В р-n – ПЕРЕХОДАХ
§ 17.1. Диффузионный р-n – переход
1. Контактная разность потенциалов
Ярким примером диффузионного контакта двух систем, рассмотренного в § 12.3, является диффузионный p-n-переход (рис.17.1). Рассмотрим кремниевый плоскостной невырожденный p-n-переход, полученный при наращивании на подложку из кремния с примесью бора – эпитаксиального слоя кремния с примесью фосфора. Концентрация электронов в области насыщения (рис.16.9) равна концентрации атомов фосфора (доноров), а концентрация дырок равна концентрации атомов бора (акцепторов) (рис. 17.1,а). Положение уровней Ферми EF определяется соотношениями (16.24) и (16.23). Уровни Ферми находятся в запрещенной зоне вблизи локальных уровней примеси, создаваемых атомами фосфора и бора. При образовании р-n–перехода происходит диффузия электронов из n-области и дырок из р-области через p-n-переход.
|
Рис. 17.1 |
Система приходит в состояние равновесия, и уровни Ферми выравниваются в областях р-n–перехода. На границе р-n–перехода образуется контактная разность потенциалов
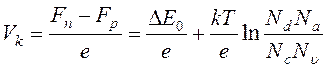 . (17.1)
. (17.1)
Из закона действующих масс (16.28) ширина запрещенной зоны
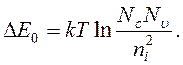 (17.2)
(17.2)
Подставим (17.2) в (17.1)
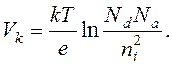 (17.3)
(17.3)
2. Соотношение Эйнштейна
При нулевом смещении (V = 0) на р-n–переходе дрейфовый ток направлен противоположно диффузионному току и общий ток через р-n–переход равен нулю:
![]() (17.4)
(17.4)
![]() (17.5)
(17.5)
где Dn
и Dp
– коэффициенты диффузии электронов и дырок; ![]() и
и ![]() –дрейфовые скорости
электронов и дырок; S – площадь р-n–перехода.
Разделяя переменные, решаем уравнения (17.4), (17.5):
–дрейфовые скорости
электронов и дырок; S – площадь р-n–перехода.
Разделяя переменные, решаем уравнения (17.4), (17.5):
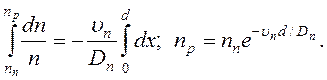 (17.6)
(17.6)
Аналогично получаем
![]() (17.7)
(17.7)
С другой стороны, из распределения Больцмана следует
![]() (17.8)
(17.8)
Сравнивая показатели выражений (17.6)...(17.8), находим соотношения Эйнштейна
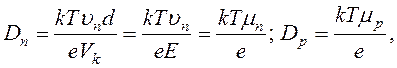 (17.9)
(17.9)
где mn и mp – подвижности электронов и дырок.
3. Инжекция основных носителей заряда через р-n–переход при положительном смещении на р-n–переходе (V > 0)
|
Рис. 17.2 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.