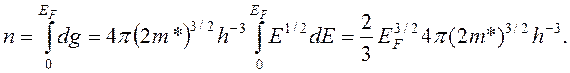Рассеяние Мандельштама-Бриллюэна. Дифракция в кристаллах. Поляризационные эффекты. Элементы статистической термодинамики. Излучение фотонов и эмиссия электронов, страница 24

             (16.14)

Отсюда

             (16.15)

2.       В собственном полупроводнике концентрация электронов равна концентрации дырок n_i= p_i.

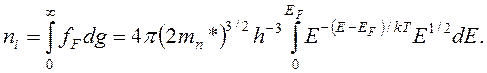
Концентрация электронов

                                              (16.16)

где N_c=2h^–3(2pm*kT)^3/2; Nc – эффективная плотность состояний в зоне проводимости.

Концентрация дырок

                                             (16.17)

где

N_u=2h^–3(2pm_p*kT)^3/2; N_u – эффективная плотность состояний в валентной зоне. Из равенства n_i= p_i следует выражение для энергии Ферми:

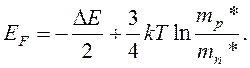                                     (16.18)

При m_p*>m_n* уровень Ферми лежит выше середины запрещенной зоны.

Из (16.16) и (16.17) концентрация носителей заряда в собственном полупроводнике

                                       (16.19)

3. В примесных полупроводниках в области насыщения, когда все примеси ионизированы, концентрация носителей заряда равна концентрации примеси

Для электронов

                                                (16.20)

Энергия Ферми

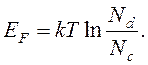                                                      (16.21)

Для дырок

                                                (16.22)

Энергия Ферми

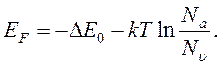                                                    (16.23)

В области низких температур (в области вымораживания) концентрация электронов определяется заменами в (16.19)

N_u ® N_d, n_i ® n, DE₀ ® E_d

                                          (16.24)

где E_d – энергия ионизации донорных атомов.

Концентрация дырок определяется аналогично:

где E_a – энергия ионизации акцепторов:

                                          (16.25)

Энергия Ферми определяется из выражений:

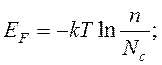                                                    (16.26)

и

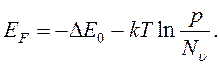                                          (16.27)

Произведение концентраций электронов и дырок в примесном полупроводнике при отсутствии вырождения

                                     (16.28)

Соотношение np = n_i² носит название закона действующих масс..

График зависимости концентрации от температуры показан на рис.16.9, где 1 – область собственной проводимости; 2 – область насыщения; 3 – область вымораживания.

С увеличением концентрации донорной примеси N, волновые функции примесных состояний электрона перекрываются, вместо локального донорного уровня образуется примесная зона и энергия ионизации доноров уменьшается.

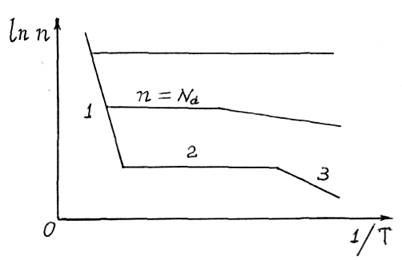
Рис.16.9

Для водородоподобных атомов примеси

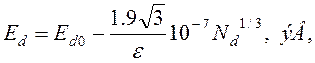                          (16.29)

где e – статическая диэлектрическая проницаемость полупроводника.

§ 16.4. Подвижность носителей заряда в полупроводниках

1. Подвижность электронов в невырожденном полупроводнике с параболичной зоной проводимости

m_n = u_n/E = et_n/m_n*,                                               (16.30)

гдеu_n и m_n* – дрейфовая скорость и эффективная масса электрона; E – напряженность внешнего электрического поля; t_n – среднее время пробега электрона (время релаксации).

Время релаксации равно отношению средней длины свободного пробега электрона к его скорости теплового движения t_n =l/u_T.

В случае рассеяния носителей заряда на колебаниях решетки (на акустических фононах) l=A/T. Скорость теплового движения

.

Подвижность электронов

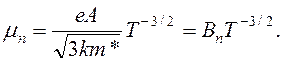                                (16.31)

Аналогичным образом зависит от температуры подвижность дырок

                                               (16.32)

Зависимости (16.31) и (16.32) удовлетворительно согласуются с экспериментом для области собственной проводимости и области насыщения слаболегированного полупроводника.

В области вымораживания превалирует рассеяние носителей заряда на ионах примеси и подвижность возрастает с повышением температуры

m_n=C_nT^3/2; m_p=C_pT^3/2.                                    (16.33)

2. В вырожденных полупроводниках и металлах энергия Ферми почти не зависит от температуры и время релаксации обратно пропорционально температуре, так как электрон вместо тепловой скорости характеризуется  фермиевской скоростью

.                                        (16.34)

Подвижность электронов в этом случае