Рассеяние Мандельштама-Бриллюэна. Дифракция в кристаллах. Поляризационные эффекты. Элементы статистической термодинамики. Излучение фотонов и эмиссия электронов, страница 12

Рассмотрим зависимость W от xпри х <<N. Воспользуемся приближением e^±x/N = 1 ± x/N. Тогда

           (13.39)

Из (13.39) видно, что при х = 0 статвес имеет резкий максимум. Соответственно энтропия подсистемы

S=k×(2N×ln 2 – 2x²/N)                                                     (13.40)

При х = 0, когда N₁ = N₂, S_max. = k×2N×ln 2.

Применяя распределение Больцмана для двухуровневой системы, запишем

,                                          (13.41)

                                           (13.42)

Отношение N₂/N₁ называется отношением населенностей уровней энергии. Когда N₂>N₁, населенность уровней называется инверсной.

При N₂>N₁, Т < 0. Отрицательная температура является температурой перехода и не характеризует термодинамическое равновесие всей системы с окружающей средой.

При N₂=N₁ температура перехода Т = ± ¥.

Реально молекулы характеризуются поступательными, колебательными и вращательными степенями свободы и температура системы положительна.

§ 13.5. Распределение Максвелла

Рассмотрим систему N атомов идеального газа в закрытом сосуде. В результате столкновений атомов между собой и со стенками сосуда устанавливается такое статистическое распределение атомов по скоростям, импульсам и энергиям, которое в силу принципа детального равновесия не будет меняться при дальнейших столкновениях. В состоянии статистического равновесия идеального газа с сосудом энтропия системы максимальна при условиях N= const, Е= const.

Для фиксированных значений импульсов распределение Больцмана (13.43)

Однако в результате столкновений импульсы атомов изменяются непрерывно. Рассмотрим дифференциальный объем 4pp²dp в пространстве импульсов (рис.13.3). Доля атомов, импульсы которых оканчиваются в пределах от р до р + dp пропорциональна 4pp²dp

                                   (13.44)

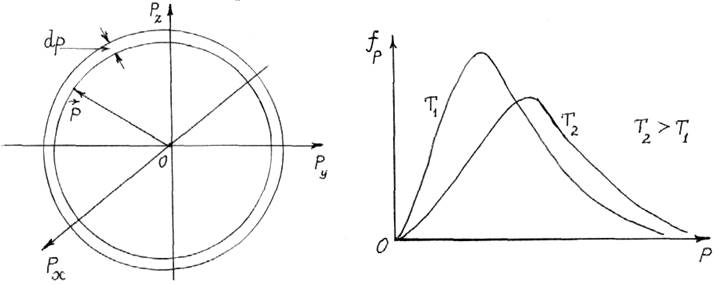
Рис. 13.3                                                      Рис. 13.4

Функция распределения атомов по импульсам (функция Максвелла) (рис.13.4)

                                (13.45)

Из условия нормировки 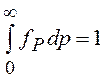 находим А:

А = (2pmkT)^-3/2.                                                     (13.46)

Заменяя в (13.45) р = mu, получаем функцию распределения молекул по скоростям (рис.13.5)

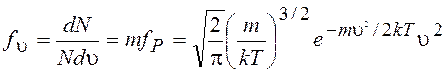                                  (13.47)

Заменяя р²/2m = E, получаем распределение атомов по кинетическим энергиям (рис. 13.6)

                (13.48)

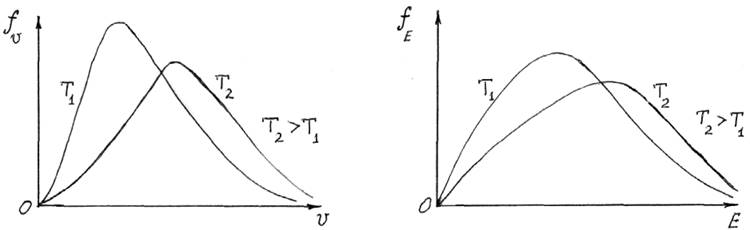
Рис. 13.5                                                     Рис. 13.6

Средняя арифметическая скорость атомов (молекул)

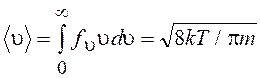                                             (13.49)

Среднеквадратичную скорость атомов определим из выражения

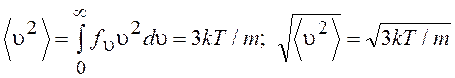                       (13.50)

Средняя кинетическая энергия атомов

                                                                     (13.51)

Наиболее вероятная скорость определяется из условия dfu/du = 0

,                                                                (13.52)

Для молекул, характеризуемых числом степеней свободы i > 3, средняя энергия

                                                              (13.53)

Случайные отклонения физических величин от их средних значений называются флуктуациями.

Простейшей мерой флуктуации величины х служит ее дисперсия s_x² или среднеквадратичное отклонение s_x. Величина флуктуации обратно пропорциональна . Если число частиц N >> 1, то отклонения физических величин от средних значений очень малы. Однако флуктуации физических величин могут существенным образом ограничивать возможности прецизионных измерительных приборов. Флуктуациями плотности среды обусловлено явление рассеяния света в различных средах.

Вопросы и задачи

1.  Построить графики зависимостей вклада одной частицы в энтропию равновесной системы от энергии фотонов при m = 0 и электронов при m = 2 эВ, Т = 300 K.

2.  Построить графики функции Ферми при Т = 0 К и Т = 300 К для свободных электронов в металле. Энергию Ферми принять равной 5 эВ.