Рассеяние Мандельштама-Бриллюэна. Дифракция в кристаллах. Поляризационные эффекты. Элементы статистической термодинамики. Излучение фотонов и эмиссия электронов, страница 23

2. Рассмотрим движение свободного электрона в периодическом потенциальном поле кристалла (16.7). Пусть электрон слабо связан с решеткой.

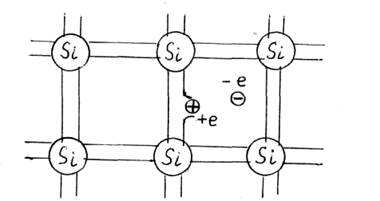
Рис. 16.6

Решение уравнения Шредингера имеет вид

                                                                 (16.6)

где  d = a + b – период решетки. Функция (16.6) – плоская волна, модулированная полем кристалла с периодом решетки (функция Блоха).

Анализ решения (16.6) при b ® 0 и U₀b= const показывает, что зависимость энергии от волнового числа претерпевает разрыв при ka = ± np (рис.16.8). Это приводит к образованию разрешенных энергетических зон, разделенных запрещенными зонами.

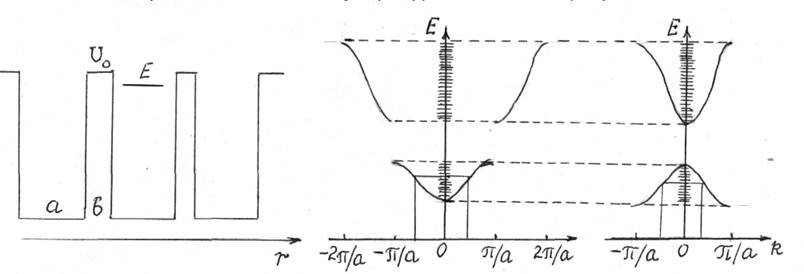
Рис. 16.7                                            Рис. 16.8

Сдвигая кривые на np/а, получаем приведенные зоны, которыми будем пользоваться в дальнейшем. Последняя из заполненных зон всегда валентная зона, а первая из свободных – зона проводимости.

Рассматриваемая задача аналогична задаче о прохождении электромагнитной волны через волновой фильтр, состоящий из LС–контуров, или через коаксиальную передающую линию с периодически расположенными диэлектрическими опорами размером b, расстояние между которыми равно а. Частотные полосы пропускания являются аналогами разрешенных энергетических зон. При выполнении условия ka = ± np или 2а = nl, происходит брэгговское отражение волн и образуются стоячие волны, которым соответствуют энергии краев запрещенных зон.

§ 16.2. Плотность квантовых состояний электронов в твердом теле

Определим плотность разрешенных квантовых состояний вблизи & = 0, считая зону проводимости параболичной

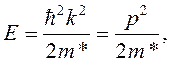                                                  (16/7)

где m* – эффективная масса электрона.

Рассмотрим прямоугольный параллелепипед, вырезанный из кристалла, со сторонами x = Na, y = Na,z = Nc. Применяя условие цикличности к функции Блоха, получаем

                                (16.8)

где l = 0,1,2,3….

Внутри зоны проводимости k_x принимает N дискретных значений

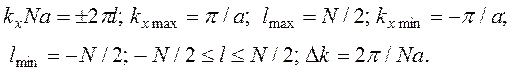
Аналогично

k_y = 2pl/Nb; k_z = 2pl/Nc; Dk_y = 2p/Nb; Dk_z = 2p/Nc; Dk_xDk_yDk_z =8p³/Nabc

Для единичного объема кристалла

Dk_xDk_yDk_z =8p³                                                      (16.9)

Умножив (16.9) на  получим выражение, согласующееся с соотношением неопределенностей Гейзенберга,

Dp_xDp_yDp_z = h³.                                            (16.10)

Согласно принципу Паули в пределах элементарной ячейки h³ в пространстве импульсов может находиться не более двух электронов. Объем шарового слоя в р-пространстве равен  4pp²dp. Число разрешенных квантовых состояний в таком слое

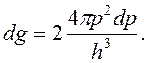                                                      (16.11)

Выразим импульс через энергию (16.7). Тогда плотность квантовых состояний пропорциональна :

dg/dE = 4p(2m*)^3/2h^-3E^1/2.                                      (16.12)

Для двумерного кристалла из (16.9) следует

Dk_xDk_y = 4p²; Dp_xDp_y = h².

Дифференциальное значение поверхности на фазовой плоскости равно 2ppdp. Поверхностная плотность квантовых состояний не зависит от энергии

dg/dE = 4pm*/h²                                                               (16.13)

Под действием внешнего магнитного поля  энергия орбитального движения свободных электронов квантована (см. § 15.2). При энергии, равной уровню энергии Ландау, плотность квантовых состояний резко возрастает. Этим обусловлены осцилляции многих физических величин, характеризующих свойства сильнолегированных (вырожденных) полупроводников и металлов.

§ 16.3. Определение концентрации свободных носителей заряда

и энергии Ферми в полупроводниках

Зная функцию Ферми (13.18) и функцию плотности состояний (16.J2), можно найти концентрацию свободных носителей заряда и энергию Ферми.

1.       В сильнолегированных полупроводниках и металлах энергия Ферми E_F>>kT и функция Ферми f_F =1. Тогда концентрация электронов в зоне проводимости равна плотности квантовых состояний