Рассеяние Мандельштама-Бриллюэна. Дифракция в кристаллах. Поляризационные эффекты. Элементы статистической термодинамики. Излучение фотонов и эмиссия электронов, страница 17

ГЛАВА 15

ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ И КВАНТОВОЙ ЭЛЕКТРОНИКИ

§ 15.1. Волны де Бройля, соотношения неопределенностей Гейзенберга

1. В квантовой механике движущейся частице соответствует волна. Волновая функция должна быть непрерывной, однозначной и конечной, чтобы определять вероятность нахождения частицы в зависимости от координат, энергии и импульса этой частицы. Согласно идее де Бройля пси-функция частицы с энергией Е = и импульсом

.                                                 (15.1)

Каждой динамической переменной в квантовой механике соответствует линейный самосопряженный оператор Q, который, действуя на пси-функцию, позволяет найти собственные значения оператора (значения динамической переменной д)

.                                                     (15.2)

Гейзенберг показал, что если операторы двух канонически сопряженных физических величин не коммутируют

, то среднеквадратичные отклонения этих физических величин

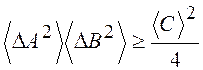                                   (15.3)

Покажем, что коммутатор операторов координаты и импульса  не равен нулю. Оператор , оператор импульса . Рассмотрим действие этих операторов на пси-функции.

                                         (15.4) 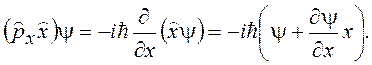                           (15.5)

Коммутатор операторов и

                                                    (15.6)

Аналогично запишем

                                       (15.7)

Соотношения (15.6) и (15.7) называются перестановочными соотношениями Гейзенберга. Среднеквадратичные отклонения координат и импульсов образуют соотношение неопределенностей Гейзенберга

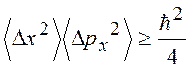
                                                      (15.8)

или

2. Применяя соотношение неопределенностей, оценим минимальную возможную энергию атома в твердом теле. Атом, совершая колебания под действием квазиупругой силы F = – kx, отклоняется от положения равновесия. Координата атома изменяется в пределах ±х, а импульс ±px . Полагая  и , из (15.8) имеем

Энергия атома (гармонического осциллятора)

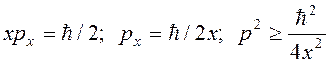                                           (15.9)

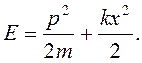                                                       (15.10)

Заменив р² из (15.9), исследуем (15.10) на экстремум

.                                                   (15.11)

Подставим (15.11) в (15.9) и (15.10):

                                 (15.12)

где w_O – собственная частота гармонического осциллятора.

При температуре T = 0 К энергия твердого тела равна сумме минимальных энергий атомов.

§ 15.2. Влияние магнитного поля на энергетический

спектр свободных электронов твердого тела

1. При помещении полупроводника или металла в магнитное поле свободные электроны под действием поля  вращаются по часовой стрелке вокруг оси Z, параллельной полю. Одна половина свободных электронов движется вдоль поля, а другая против поля по спиралям.

Покажем, что проекция орбитального момента импульса электрона L_x на ось Z квантована. Запишем уравнение для L_z:

                                                            (15.13)

где оператор .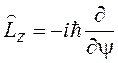

Ищем решение в виде

.                                                        (15.14)

Применим условие цикличности к пси-функции

.                          (15.15)

Отсюда

Проекция момента импульса электрона на ось Z квантована

                                                       (15.16)

Энергия электрона в магнитном поле

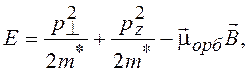                                               (15.17)

где p_z и p_^ – проекции импульса на ось Z и на плоскость, перпендикулярную оси Z; – орбитальный магнитный момент, направленный противоположно полю ,

где r – радиус орбиты; m* – эффективная масса электрона в твердом теле; w – циклотронная частота вращения электрона.

Сила Лоренца euB_^ является центростремительной силой m*wu_^ , поэтому w=eB/m*.

Преобразуем (15.17),

                       (15.18)

заменяя

p_^=m*wrи rp_^=L_z:

С учетом (15.16) энергия электрона

                                   (15.19)