Рассеяние Мандельштама-Бриллюэна. Дифракция в кристаллах. Поляризационные эффекты. Элементы статистической термодинамики. Излучение фотонов и эмиссия электронов, страница 9

Дифференцируем (12.36) по объёму газа:

                                          (12.37)

В состоянии равновесия  [см. (12.30)].

Приравняв правые части последних выражений, получаем уравнение состояния идеального газа

                       (12.38)

где M – масса моля газа; m – масса газа; R = kN_a, N_a – число Авогадро.

На основании (12.38) можно измерить температуру методом газового термометра. При постоянном объеме давление идеального газа пропорционально температуре. Выбрав реперную точку T₀ – 273,16 K, когда идеальный газ находится в термодинамическом равновесии с водой в твердой, жидкой и газообразной фазах, измеряют давление P_x. Температура идеального газа определяется из соостношения

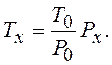                                                  (12.39)

Вопросы и задачи

1.  В чем заключается принцип детального равновесия?

2.  Какая система называется изолированной?

3.  Сформулируйте принцип равной вероятности любого квантового состояния.

4.  Какое состояние системы называется равновесным?

5.  Показать, что при диффузионном контакте двух систем частицы перемещаются из системы с высоким значением химического потенциала в систему с низким его значением.

ГЛАВА 13

СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ

§ 13.1. Вклад частицы в энтропию равновесной системы

Для получения функций распределения частиц по энергиям необходимо определить вклад одной частицы с энергией e в энтропию равновесной теплоизолированной системы, состоящей из N частиц, находящихся в замкнутом объеме V и имеющих энергию E.

В состоянии равновесия энтропия изолированной системы максимальна при дополнительных условиях:

N =const; Е = const;                                              (13.1)

Изменение энергии системы при V = const в случае теплового и диффузионного контактов (см. § 12.3)

dE=TdS+mdN                                                        (13.2)

Отсюда изменение энтропии системы

                                                  (13.3)

Из (13.3) легко получаем средний вклад частицы в энтропию системы

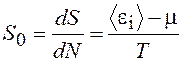,                                               (13.4)

где < e > – средняя энергия частицы.

Реально частицы имеют различные энергии e_i. Пусть ni частиц имеют примерно одинаковые энергии e_i ± de_i. Обозначим   Е_i энергию этих частиц, а S_i, – энтропию подсистемы n_i частиц. В равновесном состоянии при V = const энтропия максимальна. Тогда изменение энтропии системы равно нулю

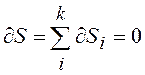;                                                      (13.5)

при

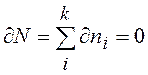                                                      (13.6)

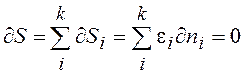,                                               (13.7)

где , ,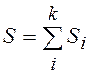

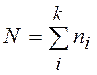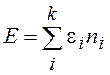
Энтропия равновесной системы равна сумме энтропии как бы встроенных друг в друга k подсистем, которые можно в силу принципа детального равновесия считать статистически независимыми. Экстремум (13.5) называют связанным, потому что на него налагаются дополнительные условия (13.1), (13.6), (13.7).

Из (13.3) следует условие максимума функции S+mN/T – E/T, поскольку

¶(S+mN/T – E/T)=0                                               (13.8)

С учетом (13.5), (13.6), (13.7) преобразуем (13.8):

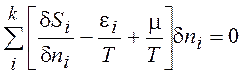                                      (13.9)

Полагая поочередно ¶n_i не равным нулю и приравнивая нулю вариации всех остальных независимых величин ¶n_i при i неравном j, получаем вклад частицы с энергией e_i в энтропию равновесной системы

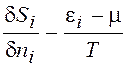,                                               (13.10)

где j = 1,2,...k.

В равновесном состоянии температура Т и химический потенциал m не зависят от энергии частицы e_j и одинаковы как для системы, так и всех подсистем

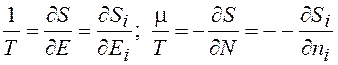.                               (13.11)

Вклад одной частицы в энтропию равновесной системы пропорционален энергии этой частицы e_j.

§ 13.2. Распределение Ферми – Дирака