Рассеяние Мандельштама-Бриллюэна. Дифракция в кристаллах. Поляризационные эффекты. Элементы статистической термодинамики. Излучение фотонов и эмиссия электронов, страница 2

При распространении гиперзвука в полупроводниках наблюдается взаимодействие фононов со свободными электронами. Если скорость когерентных фононов больше дрейфовой скорости электронов, то фононы отдают свой импульс электронам, т.е. возникает акустоэлектрический эффект.

Применение гиперзвука играет существенную роль в акустических линиях задержки в области сверхвысоких частот, а также для создания устройств акустоэлектроники и акустооптики.

§ 10.3. Дифракция в кристаллах

1. Дифракция рентгеновских лучей в кристаллах

Применяя принцип Гюйгенса, можно получить условие главных максимумов дифракции рентгеновских лучей в кристаллах.

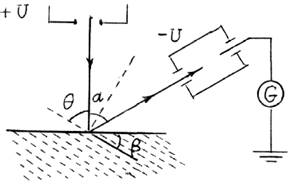
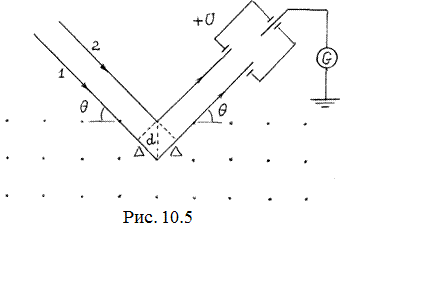Пусть рентгеновский луч падает под углом скольжения d на естественную грань кристалла (рис.10.5).

Атомы кристалла под действием рентгеновского излучения "переизлучают" вторичные волны, которые интерферируют. Показатель преломления для рентгеновских лучей равен единице, поэтому оптическая разность хода лучей равна геометрической разности хода

2=2d×sinq.                                                 (10.19)

Условие главных максимумов имеет вид

2d×sinq = ml.                                               (10.20)

где т = 1, 2, 3,..; l – длина волны излучения; (d – межплоскостное расстояние.

Выражение (10.20) называется формулой Вульфа-Брэгга.

Квантово-механическое описание дифракции рентгеновских квантов исходит из взаимодействия кванта излучения с кристаллом. При этом энергия кванта не изменяется, а импульс изменяется по направлению, но не изменяется по величине.

Запишем законы сохранения импульса и энергии для элементарного акта взаимодействия рентгеновского кванта с кристаллом (рис.10.6).

,                                              (10.21)

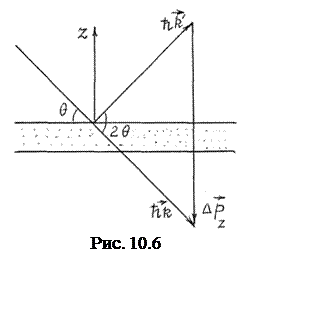
где w=w¢; k=k¢=2p/l – импульс, передаваемый кристаллу; l, – длина волны излучения.

Из треугольника (рис.10.6) видно

.                      (10.22)

Преобразуем (10.22)

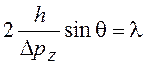.                                            (10.23)

Оценивая координату кванта с точностью до  (согласно соотношению неопределенностей Гейзенберга, см. § 15.1), получаем

.                                                         (10.24)

Сравнивая (10.24) с (10.20) видим, что с увеличением порядка главного максимума т неопределенность координаты кванта Z уменьшается.

2. Дифракция электронов

По аналогии с фотонами энергия и импульс электрона характеризуются соотношениями, называемыми дебройлевскими:

,                                      (10.25)

где – волновой вектор электрона; l – длина волны электрона. Скорость электрона равна групповой скорости волны де Бройля

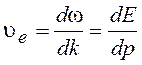.                                            (10.26)

Показатель преломления волны приближенно равен единице.

Если вместо рентгеновского луча направить пучок электронов (рис.10.5), то разность хода волн де Бройля также определяется соотношением Вульфа-Брэгга (10.20), в котором длина волны электрона

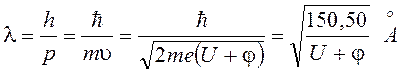,                                        (10.27)

где U – ускоряющая разность потенциалов в вольтах; l, в ангстремах, j – потенциал выхода электронов из кристалла.

Рис. 10.7

Пусть электронный пучок падает нормально на поверхность кристалла и под углом a = 55° к пучку наблюдается третий дифракционный максимум (рис.10.7). Найти соответствующее межплоскостное расстояние d, если U= 150 В. Под каким углом b к внешней поверхности ориентированы атомные плоскости? Нетрудно видеть, что b=a/2=27.5°,

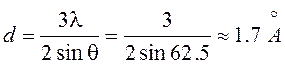
3. Дифракция света на объемной голографической решетке

Рис. 10.8

При дифракции света на объемной голограмме, полученной при интерференции двух когерентных параллельных пучков света, происходит усиление света, рассеянного поверхностями почернения (рис.10.8). В результате интерференции лучи 1, 2, 3 выходят из голограммы усиленными только под такими направлениями q_i и только таких длин волн l_i, для которых выполняется интерференционное условие