Рассеяние Мандельштама-Бриллюэна. Дифракция в кристаллах. Поляризационные эффекты. Элементы статистической термодинамики. Излучение фотонов и эмиссия электронов, страница 11

2. Рассмотрим распределение различимых частиц (атомов, молекул) по энергиям. Пусть имеется изолированная система частиц, в которой среднее расстояние l между частицами значительно больше длины волны де Бройля, соответствующей тепловой скорости частицы, т.е. при отсутствии квантового вырождения (l>>h/mu_T). Такой системой может быть идеальный газ (воздух при нормальных условиях). Эта система состоит из групп частиц. Энергия каждой группы E _i = N _ie_i, где e_i – энергия частицы i-ой группы; N_i – число частиц в группе. Энергия изолированной системы N частиц  постоянна. Число частиц . В состоянии равновесия число частиц в группах в силу принципа детального равновесия остается неизменным с точностью до флуктуации dN_i << N_i. Число частиц в каждой группе N_i >> 1. Каждую группу частиц можно рассматривать как энергетическую ячейку объемом, равным объему системы V. Выберем объем системы 7 в качестве объемной ячейки, тем самым исключим составляющую статвеса, обусловленную обменом частиц между пространственными ячейками. Частицы не взаимодействуют друг с другом на расстоянии и в основном движутся свободно, лишь кратковременно взаимодействуя при столкновениях друг с другом. Число сталкивающихся частиц мало по сравнению с числом свободно движущихся, поэтому энергия системы состоит из кинетической энергии частиц. Статвес такой системы равен числу перестановок (переходов) частиц между энергетическими ячейками системы

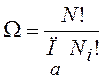,                                                   (13.24)

где а – число энергетических ячеек.

Применим формулу Стирлинга. Тогда статвес системы

                                         (13.25)

Обозначив , запишем .

Энтропия системы

,                                                     (13.26)

где

S_i=k×lnW_i=kNi×ln(N/N_i)                                (13.27)

Вклад одной частицы в энтропию системы

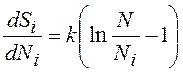.                                     (13.28)

Поскольку N>>N_i, единицей можно пренебречь. Сравнивая (13.28) и (13.10), получаем

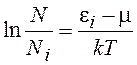                                              (13.29)

Потенцируя (13.29), получаем функцию Больцмана, характеризующую долю частиц, имеющих энергию e_i (рис 13.1):

                                   (13.30)

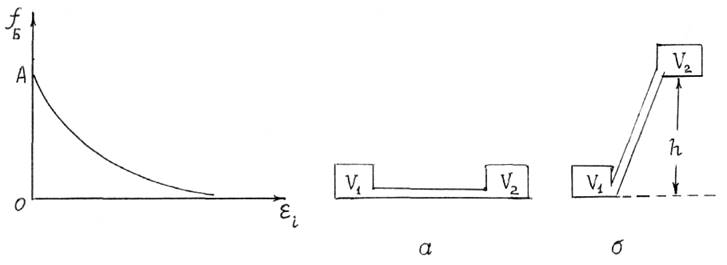
Рис. 13.1                                                      Рис. 13.2

Рассмотрим примеры применения распределения Больцмана.

1. Пусть два сосуда с идеальным газом находятся в диффузионном контакте и располагаются на высоте h = 0. (рис.13.2,а). После того как один из сосудов подняли на высоту h, энергия каждого из атомов в нем возросла на mgh и начался диффузионный процесс перехода атомов из второго сосуда в первый. Когда химические потенциалы выравнялись m₁=m₂=m, система перешла в равновесное состояние. Обозначим N. число атомов в первом сосуде, средняя энергия каждого из которых e₁; N₂ – число атомов во втором сосуде, средняя энергия каждого из которых e₂ = e₁ + mgh. Запишем функции Больцмана

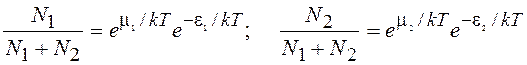.                             (13.31)

Отсюда

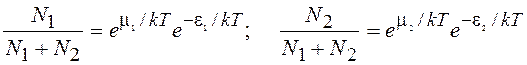.                    (13.32)

Пусть V₁=V₂=1 см³. Тогда концентрация атомов во втором сосуде

                                                   (13.33)

где n₁ – концентрация атомов в первом сосуде.

Из уравнения состояния идеального газа давление газа

.                                                    (13.34)

Умножив (13.32) на kT, получим барометрическую формулу

.                                                   (13.35)

2. Рассмотрим двухуровневую систему. Представим изолированную систему 2N молекул аммиака в равновесном состоянии. Допустим, что каждая молекула характеризуется только двумя дискретными значениями энергии E₁ и E₂ > E₁ (см. § 15.3). Число молекул с энергией Е₁ равно N₁, а с энергией E₂ равно N₂.Статвес такой подсистемы

W=(2N)!/N₁!×N₂!                                           (13.36)

Применяя формулу Стирлинга, получаем

.                                      (13.37)

Введем новую переменную

х = N₁ – N = N – N₂. Преобразуем (13.37)

                                        (13.38)