Рассеяние Мандельштама-Бриллюэна. Дифракция в кристаллах. Поляризационные эффекты. Элементы статистической термодинамики. Излучение фотонов и эмиссия электронов, страница 3

                                         (10.28)

Все остальные лучи, не удовлетворяющие этому условию, ослабляются. Если голограмму осветить белым светом, то из широкого спектра лучей голограмма самостоятельно выделит свет только длины волны l_iс высокой степенью монохроматичности и направления q_i.

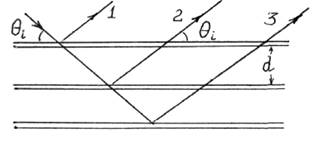
Рис. 11.7

Поэтому на стадии восстановления голограмму не обязательно освещать лазером. Можно пользоваться обычным источником света. Объемная голограмма выполняет функции монохроматора и коллиматора. В простом случае (рис.10.8) показано восстановление параллельного предметного пучка света, который при записи фронта волны в момент экспонирования был направлен под углом q_i. Интенсивность дифрагировавшего света при т>1 ослабляется, и практически наблюдается восстановление предметного пучка света только при т=1.

Вопросы и задачи

1. Получить условия главных максимумов для необыкновенной и обыкновенной волн при дифракции света на ультразвуке.

2. Почему для упругой волны (рис.10.3), направленной вдоль оси 2, частота рассеянного света увеличивается?

3. Возможна ли дифракция рентгеновских лучей в кристаллах, когда направление падающего луча перпендикулярно внешней поверх ности кристалла?

ГЛАВА 11

ПОЛЯРИЗАЦИОННЫЕ ЭФФЕКТЫ

§ 11.1. Двойное лучепреломление. Эллиптическая поляризация

Явление двойного лучепреломления состоит в том, что волны с различной поляризацией распространяются в веществе с различной скоростью. В кристаллах оптические свойства анизотропны. Это обусловлено анизотропией диэлектрической проницаемости e, являющейся тензором. Электрическая поляризация индуцированная вектором поля световой волны E_c, возникает в результате смещения зарядов. Выберем систему координат таким образом, что смещения зарядов будут направлены вдоль осей координат и параллельны электрическому полю. Тогда протекции вектора электрического смещения на оси координат

                              (11.1)

Заменяя  можно записать уравнение эллипсоида диэлектрической проницаемости

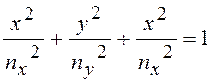                                           (11.2)

В одноосном кристалле с оптической осью вдоль направления оси z уравнение (11.2) обладает вращательной симметрией. Тогда и можно построить эллипсоид вращения (рис.11.1)

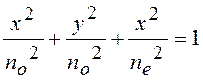
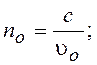
где  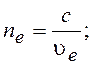n_o, n_e, u_o, u_e  – показатели преломления и скорости распространения обыкновенной (ordinaire) и необыкновенной (extraordinaire) волны.

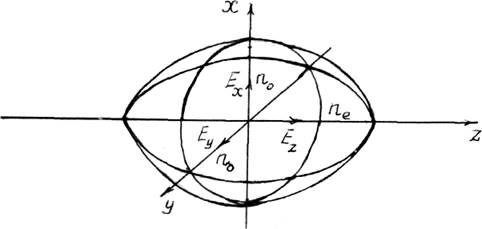
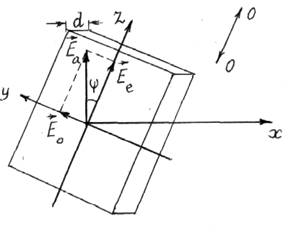
Рис. 11.1                                                      Рис. 11.2

Из рис. 11.1 видно, что плоскополяризованная волна, имеющая световой вектор, перпендикулярный оптической оси, распространяется со скоростью u_o=c/n_o, аволна, имеющая световой вектор, параллельный оптической оси, имеет скорость u_e=c/n_e. Пусть поляризованный свет распространяется вдоль направления, перпендикулярного оптической оси анизотропной кристаллической пластинки, толщиной d. Направление амплитуды световой волны составляет угол f с оптической осью кристалла (рис.11.2). Разложив  на обыкновенную и необыкновенную составляющие, имеем уравнения:

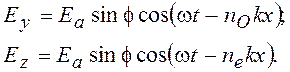                                                  (11.4)

Если после прохождения пластинки разность фаз волны составляет тс/2, то плоскополяризованная волна преобразуется в эллиптически поляризованную волну. Возводя (11.4) в квадрат и складывая, получаем уравнение эллипса

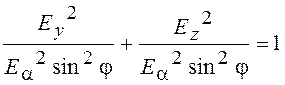                                         (11.5)

При  f = 45° конец вектора описывает окружность радиуса Е_a. В этом случае поляризация называется круговой.

Определяем минимальную толщину пластинки, при которой разность фаз волн равна p/2:

                                       (11.6)

Оптическая разность хода волн . Такая пластинка называется пластинкой в четверть волны.

При разности фаз  оптическая разность хода . Пластинка в полволны поворачивает плоскость поляризации волны на угол 2j.

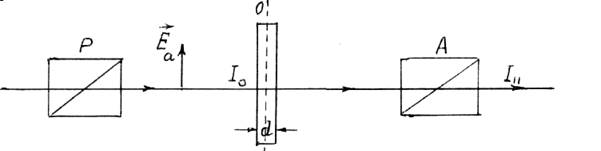
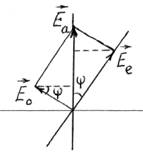
Рис. 11.3                                                                                              Рис. 11.4