В квантовой статистической теории все частицы условно можно разделить на фермионы и бозоны. Фермионы - частицы с полуцелым спином, равным 1/2, 3/2, 5/2... . Бозоны – частицы с целочисленным спином, равным 0,1,2,3… . Как фермионы, так и бозоны относятся к неразличимым (тождественным) частицам. При обмене двух тождественных частиц энергиями или местами (координатами) не изменяется число способов распределения частиц по квантовым состояниям. К фермионам применим принцип Паули, заключающийся в том, что в каждом допустимом квантовом состоянии может находиться не более одного фермиона. К фермионам относятся электроны, протоны, нейтроны и другие частицы.
Рассмотрим распределение фермионов по энергиям в равновесной системе. Для нахождения числа фермионов n i с энергией ei в квантовых состояниях z i необходимо найти функцию, характеризующую вероятность заполнения состояний ni/zi. Энтропия, характеризующая распределения n i фермионов по zi состояниям,
Si=k×lnWI(13.12)
Статвес равен числу способов распределения ni фермионов по zi состояниям
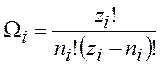, (13.13)
где zi, – число состояний в узком интервале энергий dei; n i – число фермионов, имеющих энергии ei ±dei; z i – n i — число свободных состояний в интервале dei.
Поскольку при логарифмировании (13.13) знаменатель вычитается, из рассмотрения исключаются ni! переходов в силу принципа тождественности частиц и (z i-n i)! перестановок, так как состояния zi-ni в силу принципа Паули свободны. Применяя формулу Стерлинга N!» (N/e)N при N >> 1, преобразуем (13.13):
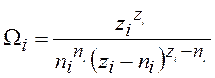(13.14)
Si=k[zi× lnzi-ni× lnni-(zi-ni)×ln(zi-ni)] (13.15)
Дифференцируя Si по ni получаем вклад одного фермиона c энергией ei в энтропию системы в равновесном состоянии
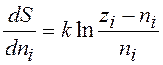. (13.16)
Учитывая (13.10), приравняем правые части (13.16) и (13.10):
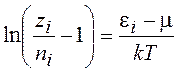. (13.17)
Потенцируя (13.17), получаем функцию Ферми-Дирака
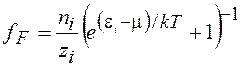(13.18)
Для свободных электронов в твердых телах химический потенциал обычно обозначают EF и называют уровнем энергии Ферми. Поскольку n i << n, azi << z, функцию Ферми обычно записывают в виде fF=dn/dz. Зная зависимость z от энергии e, можно найти число электронов в единице объема
. (13.19)
§ 13.3. Распределение Бозе-Эйнштейна.
Рассмотрим систему, состоящую из бозонов, например фотонов, в равновесном состоянии. Статвес для подсистемы, состоящей из ni бозонов с энергией ei, распределенных по состояниям z i, запишем в виде
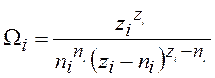(13.20)
Бозоны не подчиняются принципу Паули, поэтому в одном квантовом состоянии может находиться любое количество бозонов и статвес определяется числом перестановок объектов ni+zi. Однако из рассмотрения надо исключить один объект, относительно которого начинается расчет статвеса. Тогда из числа перестановок (ni+Zi-1)! исключаем взаимные перестановки состояниями (zi – 1)! и взаимные обмены бозонами ni!.
Применим к (13.20) формулу Стирлинга при ni >> 1 и zi>>1:
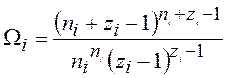(13.21)
Подставляя (13.21) в (13.12), логарифмируя, дифференцируя, сравнивая с (13.10), затем потенцируя, получаем функцию Бозе - Эйнштейна
,
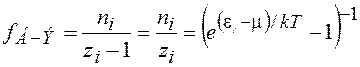(13.22)
характеризующую вероятность заполнения состояний бозонами (фотонами, фононами, ...).
§ 13.4. Распределение Больцмана
1.В частном случае, когда энергия частицы e>>m, в квантовых распределениях (13.18) и (13.22) можно пренебречь единицей по сравнению с экспонентой.
Тогда получаем функцию Больцмана
(13.23)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.