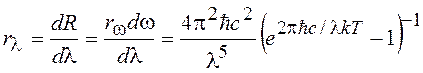Рассеяние Мандельштама-Бриллюэна. Дифракция в кристаллах. Поляризационные эффекты. Элементы статистической термодинамики. Излучение фотонов и эмиссия электронов, страница 14

                            (14.12)

В низкочастотном (длинноволновом) пределе, когда <<kT, . Тогда из (14.9) и (14.10) следует классическая формула Рэлея–Джинса

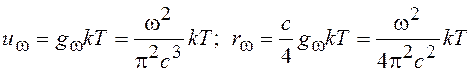                    (14.13)

В этом проявляется принцип соответствия, согласно которому квантовая теория теплового излучения включает классическую теорию как предельный случай при ® 0. При этом квантово-механическое описание теплового излучения эквивалентно классическому, когда энергии излучаемых квантов настолько малы, что частоту излучения допустимо считать непрерывной переменной.

Зависимость спектральной светимости от длины волны излучения представлена рис. 14.3, где 1 – функция Планка; 2 – функция Рэлея-Джинса; 3 -эксперимент. Дифференцируя (14.12), получаем закон Вина

,                                           (14.14)

где b = 2.90^.10³ мК.

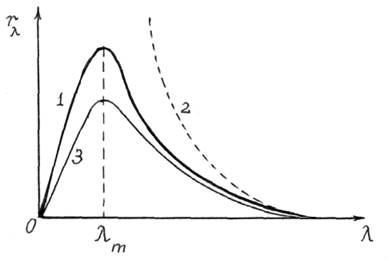
Рис. 14.3

§ 14.3. Вынужденное излучение

Из квантовой теории следует, что энергия атомов твердого тела изменяется дискретно (прерывно).

Согласно принципу детального равновесия при постоянной температуре твердого тела число переходов атомов в секунду с энергетического уровня E_n на уровень E_m равно числу обратных переходов с уровня Е_m на уровень Е_n. Пусть число атомов с энергией E_n равно N_n, а с энергией Е_m равно N_m. Разность энергий атомов Е_m - Е_n = w.

Равновесное распределение атомов по энергиям определяется функцией Больцмана

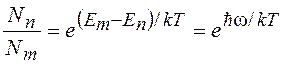.                               (14.15)

Подставим (14.15) в (14.5):

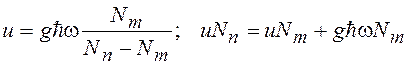.                   (14.16)

Эйнштейн постулировал существование вынужденного излучения, индуцируемого внешним вынуждающим излучением. Число вынужденных переходов атомов в единицу времени с более высокого уровня энергии Е_m на низкий уровень Е_n пропорционально произведению плотности вынуждающего излучения на число возбужденных атомов N_m:, где В - коэффициент Эйнштейна.

Направление, частота, фаза и поляризация вынужденного излучения полностью совпадают с соответствующими характеристиками вынуждающего излучения. Следовательно, вынужденное и вынуждающее излучения оказываются строго когерентными.

Число обратных вынужденных переходов атомов в единицу времени, вызванных поглощением фотонов энергией ,

.

Число спонтанных (самопроизвольных) переходов атомов в единицу времени с высокого уровня Е_m на низкий уровень Е_n пропорционально числу возбужденных атомов

.

Спонтанное излучение не является когерентным. Умножая (14.16) на коэффициент Эйнштейна, видим, что принцип детального равновесия согласуется с (14.5)

.

Отсюда следует, что А = Вg.

Заметим, что статистические распределения, в свою очередь, были получены в гл.13 на основании принципа детального равновесия.

При N_n/N_m = 2 в каждом квантовом состоянии имеется по одному фотону и лишь треть атомов находится в возбужденном состоянии, а вероятности вынужденного и спонтанного излучений равны друг другу. При N_n = N_m вероятности вынужденного излучения и поглощения одинаковы, а спонтанное излучение отсутствует. Если каким-либо образом удается возбудить атомы и добиться выполнения условия N_n > N_m, называемого условием инверсии населенностей, то вероятность вынужденного излучения превалирует над вероятностью вынужденного поглощения и физическая система может излучать вынужденно фотоны с энергией E_m–E_n.

В этом случае вещество не находится в равновесном состоянии с излучением, а температура, определяемая соотношением (14.15), отрицательна и называется температурой перехода. Однако температура вещества остается положительной.

§ 14.4. Термоэлектронная эмиссия. Закон Ричардсона-Дэшмана

Явление термоэлектронной эмиссии заключается в испускании электронов нагретыми металлами и полупроводниками. Это явление представляет собой основной источник электронов в вакуумных электронных приборах, люминесцентных лампах, а также во многих приборах для научного исследования.

При нагревании эмиттера (катода) энергии некоторых свободных электронов увеличиваются настолько, что эти электроны преодолевают потенциальный барьер на поверхности эмиттера и, совершая работу выхода, вылетают с поверхности. Поэтому эмитируемый электрон должен иметь энергию, связанную с движением в направлении х (рис. 14.4)