Рассеяние Мандельштама-Бриллюэна. Дифракция в кристаллах. Поляризационные эффекты. Элементы статистической термодинамики. Излучение фотонов и эмиссия электронов, страница 19

При туннелировании молекулы сквозь барьер амплитуды вероятности перехода из состояния 1 в состояние 2 и из состояния 2 в состояние 1 равны. Соответствующие матричные элементы гамильтониана равны друг другу и характеризуют изменение энергии молекулы при туннельном переходе

H₁₂ = H₂₁ = DE = – |DE |.

Знак "минус" выбран для удобства. Тогда вместо уравнений (15.31) получаем пару взаимно зависимых уравнений:

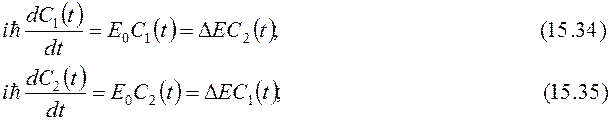
Для упрощения опустим признак зависимости амплитуд C от времени.

Складывая и вычитая уравнения (15.34) и (15.35), получаем два независимых уравнения

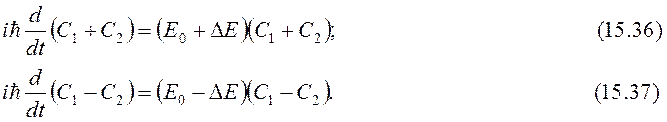
Решения этих уравнений

где E₀ + DE = E₁; E₀ – DE = E₂. Напомним, что E₂ > E₁и  DE < 0.

При C₁ = C₂ реализуется состояние с энергией E₁, а при C₁ = –C₂ – c энергией молекулы E₂.

Складывая и вычитая (15.38) и (15.39), получаем

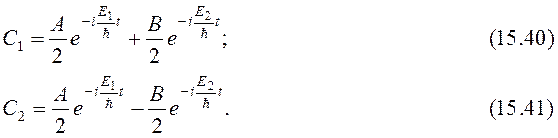
Если при t=0 молекула находится в состоянии 1, то C₁(0) = 1, C₂(0) = 0.

Значит, C₁(0) = (A+B)/2 = 1, C₂(0) = (A – B)/2 = 0. Отсюда следует, что A = B = 1.

Преобразуем (15.40) и (15.41), применив формулу Эйлера:

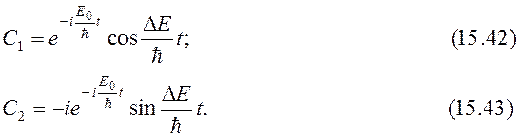
Вероятность того, что молекула будет обнаружена в состоянии 1, равна квадрату модуля C₁(t):

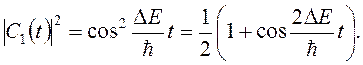                            (15.44)

Аналогично находим вероятность пребывания молекулы в состоянии 2:

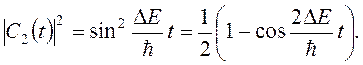                            (15.45)

Частота инверсионного перехода находится в области СВЧ и равна 24870 МГц. Линейные уравнения (15.34) и (15.35) аналогичны уравнениям для связанных гармонических осцилляторов (см. § 8.5). Однако расщепление колебательных уровней энергии в молекулах аммиака обусловлено туннельным эффектом, не имеющим аналога в классической механике.

2. Инверсия населенностей

Определим число молекул аммиака с энергиями E₁ и E₂. Из распределения Больцмана следует, что числа молекул с энергиями E₁ и E₂ соответственно

                            (15.46)

Отношение N₁/N₂

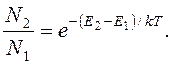                                                  (15.47)

При N₁ < N₂, T < 0 K, так, как E₂ > E₁.

Отрицательная температура не является термодинамической и не характеризует тепловое равновесие физической системы с окружающей средой, а является температурой перехода молекулы с уровня E₁ на уровень E₂ и обратно, когда остальные переходы (степени свободы) условно считаются "замороженными". Обычное состояние вещества, находящегося в термодинамическом равновесии с окружающей средой, характеризуется только положительной температурой Т > 0 K, когда N₁ > N₂.

Состояние вещества, в котором для некоторых уровней энергии выполняется условие, называется инверсным или состоянием с инверсией населенностей N₂ > N₁ и является необходимым условием для работы любого квантового генератора (лазера). Осуществление инверсии населенностей в пучковом квантовом генераторе (аммиачном лазере) проводится в постоянном во времени, но неоднородном в пространстве электрическом поле . Молекулы аммиака обладают электрическим дипольным моментом  Если  параллелен , то энергия молекул уменьшается. Напомним, что энергия диполя определяется скалярным произведением  и  взятым с отрицательным знаком. Такие молекулы втягиваются в область сильного электрического поля. Молекулы с антипараллельным направлением  и поля  выталкиваются в область слабого поля и имеют большую энергию (см. рис.15.3).

3. Расщепление уровней энергии в молекуле аммиака в электрическом поле

Предположим, что потенциальный барьер между минимумами отсутствует. Тогда энергии молекул в электрическом поле  отличаются на энергию диполя в поле  и матричные элементы гамильтониана равны:

H₁₁ = E₀ - p_eE; H₂₂ = E₀ + p_eE.                               (15.48)

Реально при туннельном эффекте сквозь барьер происходит изменение энергии молекулы на величину DE. Электрическое поле не изменяет существенно геометрии молекул, и можно принять матричные элементы