Рассеяние Мандельштама-Бриллюэна. Дифракция в кристаллах. Поляризационные эффекты. Элементы статистической термодинамики. Излучение фотонов и эмиссия электронов, страница 6

После прохождения активного вещества происходит суперпозиция волн. Складывая проекции на ось х, получаем

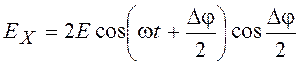.                                               (11.27)

Для проекции на ось y имеем выражение

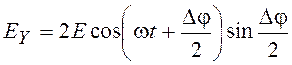.                                                 (11.28)

Разделив (11.28) на (11.27), получим уравнение движения конца вектора

                              (11.29)

Конец вектора  совершает колебание по прямой, образующей с осью хугол .

Две волны, поляризованные по кругу в противоположном направлении, на выходе из активного вещества дают результирующую плоскополяризованную волну, плоскость поляризации которой повернута по отношению к плоскости поляризации падающей волны на угол . Тогда

                                              (11.30)

Разность показателей преломления  в области не очень сильных полей линейно зависит от напряженности магнитного поля, и в общем виде угол фарадеевского вращения q описывается соотношением (11.22). Для сильно легированных полупроводников

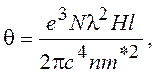                                           (11.31)

где N – концентрация свободных электронов; l, – длина волны излучения; п–показатель преломления при H=0; т* - эффективная масса свободных электронов; с – скорость света; е - заряд электрона.

Вопросы и задачи

1.  Определить толщину пластинки (рис.11.2), при которой плоскополяризованная волна преобразуется в эллиптически поляризованную.

2.  Анизотропная пластинка в четверть волны помещена между скрещенными поляризаторами. Направление амплитуды световой волны Е составляет угол j = 45° с оптической осью пластинки. Определить интенсивность света, прошедшего анализатор, если интенсивность света, прошедшего первый поляризатор, равна I. Для передачи телевизионного сигнала с помощью лазерного луча используется ячейка Поккельса на основе кристалла арсенида галлия. При напряжении на ячейке 300 В в полосе частот 5 МГц получается 100-процентная модуляция лазерного излучения с длиной волны 1,06 мкм. Показатель преломления арсенида галлия п = 3,34, электрооптический коэффициент r = 1,6×10^-10 см/В. Найти разность фаз волн после прохождения ячейки.

ГЛАВА 12

ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ

Законы термодинамики легко можно получить из принципов статистической механики, неполным выражением которых они являются.

Дж. Гиббс, 1902 г.

§ 12.1. Основные принципы статистической физики

Статистическую термодинамику легче изучать с позиций квантовой механики. Основное понятие, используемое при таком подходе, – понятие о стационарном квантовом состоянии системы, при котором все наблюдаемые физические величины не зависят явно от времени.

Методы рассмотрения статистических закономерностей основаны на постулате равной вероятности, заключающемся в том, что изолированная система может находиться с равной вероятностью в любом допустимом стационарном квантовом состоянии.

На базе постулата равной вероятности можно построить полную теорию равновесных макроскопических систем. Зная число допустимых квантовых состояний системы, называемых статистическим весом W. можно определить энтропию системы как логарифм числа квантовых состояний. Энтропия является самой важной физической величиной в статистической термодинамике. Так, с помощью энтропии можно определить как интенсивные величины - температуру, химический потенциал, так и аддитивные величины - термодинамические потенциалы.

В квантовой статистической физике все энергетические состояния в интервале энергий dE_i, вблизи уровня энергии Е_i. Равновероятны и характеризуются статвесом W_i. Состояние статистического равновесия характеризуется максимальным значением числа допустимых состояний W_max. В состоянии равновесия число частиц N_iв каждой из групп частиц от времени явно не зависит. Это обусловлено принципом детального равновесия, согласно которому в равновесной изолированной системе каждый микропроцесс сопровождается обратным ему процессом, причем вероятность обоих процессов одинакова. Такими процессами, в частности, являются прямые и обратные квантовые переходы частиц из одного энергетического состояния в другое. Это позволяет считать каждую из групп частиц N_^ системы как статистически квазинезависимую подсистему. Тогда статвес системы в равновесном состоянии равен произведению статвесов подсистем