Рассеяние Мандельштама-Бриллюэна. Дифракция в кристаллах. Поляризационные эффекты. Элементы статистической термодинамики. Излучение фотонов и эмиссия электронов, страница 18

Энергия движения электрона по круговой орбите квантована. Составляющая энергии движения электрона вдоль поля  изменяется непрерывно. Для перехода электрона с одной орбиты на другую энергия электрона изменяется на . Квантованные уровни энергии электрона в твердом теле, помещенном в магнитное поле  называются уровнями Ландау.

2. Применяя соотношение неопределенностей, оценим минимальную энергию вращения электрона в поле  по круговой орбите. Полагая p_z = 0 Dr » r и Dp_^» p_^, получаем . Энергия электрона при p_z=0

.                                       (15.20)

Исследуя (15.20) на экстремум, имеем

.                                            (15.21)

Полная энергия свободного электрона, движущегося в магнитном поле в кристалле, например, полупроводника

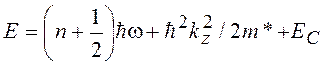,                        (15.22)

где k_z – проекция волнового вектора электрона на ось Z; E_C – энергия дна зоны проводимости полупроводника.

3. Рассмотренная задача имеет точное решение. Из теории электромагнитного поля следует, что импульс электрона в поле

, где  – векторный потенциал. Индукция магнитного поля . Когда полепараллельно оси Z, тогда B_z=B, B_y= B_x=0.

Соответственно калибровка для векторного потенциала .

Уравнение Шредингера для электрона в магнитном поле имеет следующий вид:

                                                               (15.23)

гдеоператор Гамильтона

                                (15.24)

где операторы проекций импульса

Магнитная сила является центростремительной силой Тогда

Преобразуем гамильтониан задачи и запишем уравнение Шредингера

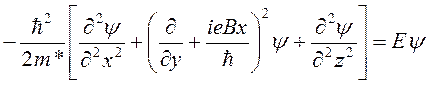.                          (15.25)

При B=0 решение имеет вид

                                               (15.26)

при В ¹ 0 решение (15.25) можно искать в виде суперпозиции

.                                                  (15.27)

Подставив (15.27) в (15.25) и сократив на экспоненту, получим уравнение гармонического осциллятора

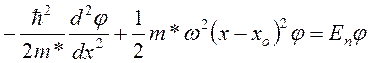,                          (15.28)

где

.

Энергия E_n принимает квантованные значения

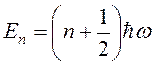,                                                    (15.29)

где n = 0,1,2,3,…; E_n – уровни Ландау.

§ 15.3. Квантовый генератор на молекулах аммиака

1. Расщепление колебательных уровней энергии

на подуровни в молекулах аммиака

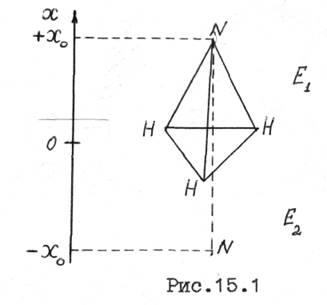
Молекула аммиака NH₃ обладает двумя устойчивыми расположениями атомов (равновесными конфигурациями) (рис.15.1).

Колебательные уровни молекул аммиака связаны с колебаниями атомов в молекулах. Каждый колебательный уровень расщепляется на два подуровня, называемых инверсионными. Расщепление уровней обусловлено тем, что потенциальная энергия молекулы и как функция расстояния х атома азота от плоскости атомов водорода имеет два минимума (рис.15.2).

              

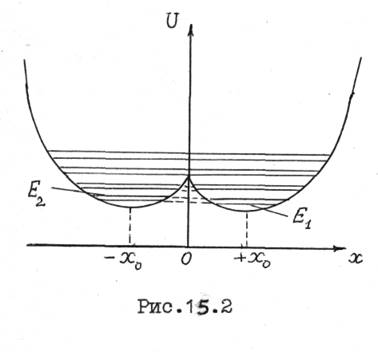
При малых отклонениях от положения равновесия (x = ±x₀) происходят колебания молекулы относительно этих положений. В квантовой механике возможен переход из одного минимума в другой, где энергия молекулы меньше ее потенциальной энергии U. Такой переход сквозь потенциальный барьер обусловлен туннельным эффектом. В результате при переходе вместо двух независимых колебательных уровней с одинаковой энергией E₀ в каждом минимуме появляются два близких уровня энергии E₁ и E₂ (рис.15.2), общих для обоих минимумов. Между этими уровнями возможен инверсионный переход с излучением фотона частотой n= (E₂ – E₁)/h.

Найдем вероятности пребывания молекулы аммиака в состояниях с энергиями. Нас не интересует местонахождение молекулы. Согласно принципу E₂ – E₁ суперпозиции состояний запишем волновую функцию состояния молекулы аммиака

                           (15.30)

где С₁(t) и С₂(t) – амплитуды вероятности пребывания молекулы в состояниях с энергиями E₁ и E₂ .

Предположим, что потенциальный барьер между минимумами отсутствует, тогда уравнения Шредингера имеют простейшую матричную форму

                  (15.31)

Матричные элементы гамильтониана равны друг другу и решения уравнений одинаковы H₁₁=H₂₂=E₀,

.                                                (15.32)