Координация изоляции электрооборудования: Учебное пособие к практическим занятиям, страница 45

За время от t до t + dt в n ИК в среднем появится dn_g = a n dt Из них откажут до очередного контроля, т.е. до момента времени Т_и, и вызовут аварии те, у которых t₀ < Т_и – t. Вероятность того, что t₀ < Т_и – t равна, очевидно, F₀(T_и – t). Поэтому число таких аварийных исходов равно dn_a1 = a n F₀(T_и – t) dt. Кроме того, часть дефекных Ик останутся невыявленными до времени контроля и вызовут аварии уже после испытаний. Их число будет dn_a2 = a n (1 - h) (1 – F₀(T_и - t)) dt. Суммарное число аварийных исходов от дефектов за интервал времени dt будет dn_a - dn_a1 + dn_a2 = a n (F₀(T_и – t) +

(1 - h) (1 – F₀(T_и – t))) dt - a n (1 - h + h F₀(T_и – t)) dt. Тогда полное число аварийных исходов от дефектов, появившихся за период времени Ти между испытаниями, составит

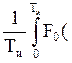n_a = a n 1 - h + h F₀(T_и – t)) dt = a n ((1 - h) T_и + h₀ F₀(t) dt = a n T_и(1 - h (1 - t) dt                             (7.8)

Общее число дефектов, образовавшихся за время Т_и, равно в среднем n_g = a n T_и. Поэтому эффективность периодического контроля или доля своевременно выявляемых дефектных ИК определяется выражением

91

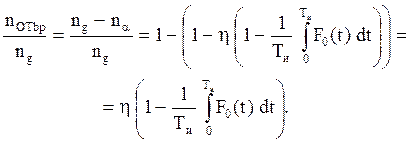    (7.9)

Соотношения (7.8) и (7.9) можно использовать для выбора экономически оптимального интервала времени Т_{и опт} между испытаниями. Если стоимость контроля одной ИК равна С_ио, а средний ущерб от одной аварии, вызванной внезапным отказом (пробоем) ИК, составляет С_aо, то суммарные затраты, отнесенные к единице времени, будут равны  или с учетом (7.8) имеем

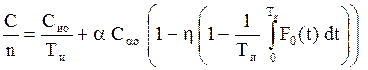           (7.10)

Тогда условие  для определения значения Т_{и опт} имеет вид

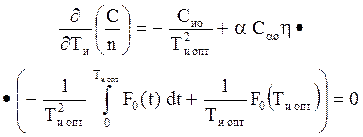
или                     Т_{и опт} F(Т_{и опт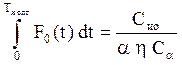}) -  .             (7.11)

Отсюда следует, что не всегда величина Т_{и опт} имеет конечное значение. В самом деле, левая часть (7.11) численно равна заштрихо

92

ванной площади рис. 7.1, которая при Т_и ® ¥ стремится к некоторому конечному пределу S. Например, если все значения t₀ в интервале от0 до t_{0 max} равновероятны, т.е. F₀(t) = t / t_{0 max} , то S = t_{0 max} / 2.

Поэтому, если правая часть (7.11) С_ио / a С_aо h >S

1   F0(t)

t 

0

Т_{и опт}

Рис. 7.1. К оценке оптимального интервала между

испытаниями

(сравнительно малый ущерб от аварий, малое появление дефектов или высокая стоимость проведения испытаний), то условие (7.11) не может быть соблюдено и минимуму затрат соответствует Т_и ® ¥. Это означает, что система периодического контроля экономически невыгодна и испытания в процессе эксплуатации проводить не следует. Зависимость C / n = f(T_и) в области минимума затрат (если он существует) может изменяться медленно. Поэтому интересно определить область значений Т_и, в которой C / n отличается от минимальной не более, чем в g раз. Эту задачу решим для случая, когда все значения t₀ от 0 до t_{0 max} равновероятны и F(t) = t / t_{0 max} . В этом случае

. Условие для определения оптимального значения имеет вид 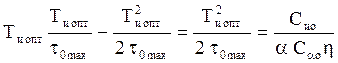. Откуда имеем

93

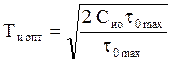. Далее положим h = 1,0. При этом минимальные затраты составят 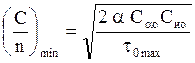. Следовательно, для определения области значений Т_и необходимо решить уравнение 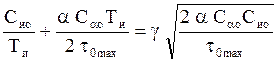. Его решение равно Т_и1,2 = Т_{и опт} (g ± ). Численные значения Т_и1,2 / Т_{и опт} для разных g приведены в табл. 7.1.

Таблица 7.1

Затраты от интервала времени контроля ИК

Из табл. 7.1 видно, что в данном частном случае сокращение или увеличение интервала времени Т_и в два раза против оптимального дает повышение затрат, по сравнению с минимально возможными, всего лишь на 25%. Это означает, что и в реальных условиях экономически целесообразный интервал между испытаниями может быть очень неопределенным и при изменении Т_и в сравнительно широких пределах суммарные затраты могут меняться незначительно.