Координация изоляции электрооборудования: Учебное пособие к практическим занятиям, страница 29

водная , позволяет определить для разных моментов время p₁ t. При интенсивной внешней ионизации, когда p₁ и i не зависят от времени, выражение (5.37) преобразуется в линейную зависимость  наклон которой пропорционален p₁ i ,а средне статистическое время согласно (5.36) обратно пропорционально p₁ i . Измеряя тангенс угла наклона экспериментальной зависимости ln(n_t / n₀) или среднее статистическое время при различных напряженностях электрического поля, можно определить то напряжение, при котором вероятность р₁ близка к единице. При р₁ = 1 имеем ln(n_t / n₀) = i, а t_c = 1 / i, и если i = const, то с увеличением напряжения угол наклона и время запаздывания перестают зависеть от напряженности электрического поля в промежутке. Следовательно, величина напряжения, при которой ln(n_t / n₀) и не зависит от напряженности поля, и является тем порогом, при котором каждый электрон, появившийся в промежутке, является эффективным.

ХАРАКТЕРИСТИКИ ПРОБИВНЫХ

 НАПРЯЖЕНИЙ ПРОМЕЖУТКОВ

Теоретическое определение закона распределения разбросов пробивных напряжений позволяет выявить и проследить влияние различных факторов на этот закон. Рассмотрим газовый промежуток с резконеоднородным электрическим полем, закон изменения напря

55

КРИТЕРИЙ КОЛМОГОРОГО. В качестве меры расхождения между теоретическим F(x) и статистическим  распределениями принимается максимальное значение модуля разности между значениями чисел в этих рядах:

 .                          (5.18)

А.Н. Колмогоров доказал, что при любой функции распределение F(x) непрерывной случайной величины Х и при неограниченном возрастании числа независимых наблюдений n вероятность выполнения неравенства

                                       (5.19)

стремится к пределу  Значения l, соответствующие определенным уровням значимости ) приведены в табл. 5.5.

Таблица 5.5

Уровни значимости для критерия согласия Колмогорова

Cхема применения критерия Колмогорова следующая:

1. По несгруппированному статистическому ряду строится функция распределения (х).

42

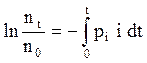                                (5.34)

или 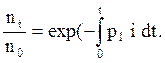                                                              (5.34.a)

Полученная функция показывает, какая часть общего числа разрядов произойдет при времени больше t, т.е. какая часть разрядов будет иметь время t_c > t. При достаточно большом числе n₀ это будет функцией распределения вероятностей статистического времени запаздывания разряда:

P(t_c > t) = exp(-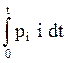)                        (5.34.b)

В том случае, если i и р₁  постоянные величины, то

P(t_c > t) = exp(-p₁ i t),                                (5.35)

причем среднее статистическое время запаздывания равно

                                      (5.36)

Если учесть время формирования разряда t_¥, то (5.34) запишется:

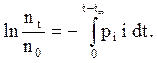                           (5.37)

Выражения (5.34) и (5.37), известные как выражения Лауэ, интересны тем, что, имея экспериментальную зависимость ln(n_t / n₀) = f(t), можно оценить различные характеристики разряда. Например, минимальное время запаздывания согласно (5.37) равно t_ф, а произ

54

2. Строится теоретическая функция F(х) . Если числовые характеристики этой функции неизвестны, то используются их оценки из опытных данных.

3. Определяется максимальное отклонение по (5.17).

4. Вычисляется величина

5. Задается уровень значимости a₁ и из табл. 5.5 определяется соответствующий параметр l_a.

6. Сравниваются l и l_a. Если l £ l_a, то гипотеза о соответствии  и F(x) считается правдоподобной с уровнем значимости a₁, в противном случае гипотеза отвергается.