Координация изоляции электрооборудования: Учебное пособие к практическим занятиям, страница 26

РАСПРЕДЕЛЕНИЕ ПУАССОНА. Если в биноминальном распределении положить, что r ® 0, а n ® ¥ , причем  n r = a = сonst, то вероятность наступления события ровно m раз в серии из n испытаний равна

Это и есть закон Пуассона или распределение редких событий

                                       (5.17)

В (5.17) распределение зависит от одного параметра a, который равен одновременно и матожиданию, и дисперсии случайной ве

37

пряжения всей изоляционной конструкции, состоящей из n параллель ных элементов. Примем, что пробои отдельных элементов независимые и совместимые события. Тогда по теории сложения вероятностей  определяем функции распределения для пробивного напряжения всей изоляционной конструкции

                       (5.43)

В случае, когда вероятности пробоя всех элементов одинаковы - = F₁(U), выражение (5.43) приводится к виду

F_n(U) = 1 - .                     (5.44)

При достаточно большом числе параллельно включенных элементов распределение (5.44) стремится к экспериментальному распределению. Тип последнего определяется видом распределения F₁(U).

Можно, однако сделать ряд  упрощений, при которых получаются важные практические выводы. Выполним возведение в степень в (5.44):

F_n(U) = n F₁(U) .

Если вероятность F₁(U)  мала, что F₁(U) << 1 / n, тогда

                                F_n(U) »n F₁(U)                                         (5.45)

Малые вероятности F₁(U) соответствуют малым пробивным напряже

59

личины Х:      Отсюда находим высшие моменты m₃ = a, m₄ = 3 a² + a и коэффициент асимметрии S_k =1/ и эксцесса E_х = 1/a.

Применение распределения Пуасона.

1. В теории надежности, для n одинаковых элементов с экспоненциальным законом распределения времени безотказной работы случайное число отказов Х элементов за время t при большом n и малой вероятности отказов каждого элемента распределено по закону Пуасона с параметром   a = n l t, где l - интенсивность отказов.

2. Закону Пуасона подчиняются многие физические явления. Например, пусть с накаленного катода за единицу времени влетает в среднем u(t) электронов. Тогда вероятность того, что за интервал времени(t_о, t_о + Dt) вылетает ровно m электронов, подчиняется распределению Пуасона с параметром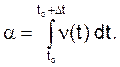

3. Такой закон хорошо аппроксимирует биноминальное распределение в случае, когда r << 1, т.е. когда математическое ожидание мало отличается от дисперсии ( n p » n p (1-p)). Таблицы распределения в /2/.

5.2. КРИТЕРИИ СОГЛАСИЯ КОЛМОГОРОВА И ПИРСОНА.

После систематизации опытных данных и вычисления числовых характеристик необходимо определить (подобрать) теоретический

38

ным измерений сводится к решению задачи об оценке вероятности случайного события по его частости. Многочисленные опыты показали, что зависимость вероятности разряда от амплитуды воздействующего напряжения Uм описывается функцией нормального закона распределения случайных величин

P(U_м) = 0,5 + Ф(),                     (5.41)

где  - значение амплитуды напряжения при P(U) = 0,5; s - мера крутизны зависимости P(U_м), которая определяется как средне квадратическое отклонение для напряжения и согласуется с экспериментами для нормальной функции в пределах U_м ± 3s. Таким образом, в общем случае вероятностной характеристикой пробивных напряжений является закон распределения F(U) = P(U_пр < U) или P(U_м < U) с основными числовыми характеристиками  или  и s.

ОЦЕНКА ЭЛЕКТРИЧЕСКОЙ ПРОЧНОСТИ ИЗОЛЯЦИОННОЙ

КОНСТРУКЦИИ ПО ЭЛЕКТРИЧЕСКОЙ ПРОЧНОСТИ

 ОТДЕЛЬНЫХ ЕЕ ЭЛЕМЕНТОВ

Изоляционная конструкция – это композиция из однородных элементов. Рассмотрим применительно к такой конструкции решение следующей задачи. У отдельных i –x элементов измерены пробивные напряжения Uпр, а также определены функции распределения пробивного напряжения

.                             (5.42)

Требуется определить вероятностные характеристики пробивного на

58

закон распределения, наилучшим образом характеризующий вероятностные закономерности статистического ряда.

Здесь возникает две задачи.