Координация изоляции электрооборудования: Учебное пособие к практическим занятиям, страница 24

62

статистики исследуется случайная величина Т = Х где величина Х и c² независимы,  Х  распределена по нормальному закону с параметрами  m = 0,     s = 1, а c² распределена по закону Пирсона с  r  степенями свободы. Распределение такой случайной величины  Т  носит название  Стьюдента, с плотностью распределения f(x) = 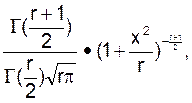матожиданием m = 0  и дисперсией , где r степень свободы. Распределение Стьюдента широко используется в математической статистики при анализе опытных данных. Его удобство заключается в том, что оно связано только с числом степеней свободы r , т.е., если говорить об экспериментальных данных, с число измерений. При r > 30 распределение Стьюдента мало отличается от нормального, поэтому его используют для оценок вероятности попадания случайной величины в заданный интервал.

            Вид распределения Стьюдента приведен на рис. 5.6.

                                             f(x)

0                               x

Рис. 5.6. Распределение случайных величин по Стьюденту

БИНОМИНАЛЬНОЕ РАСПРЕДЕЛЕНИЕ. Такое распределение

35

присутствии дефекта в изоляции, напротив, вероятность появления максимального напряжения пробоя – это отсутствие дефекта в изоляции или пробой его при высоком пробивном напряжении хотя бы одного образца из десяти испытанных. 50 % - ая вероятность пробивного напряжения служит значением для выбора рабочего напряжения аппарата, в котором возможно использовать изоляционный материал. Для этого достаточно найти электрическую прочность испытуемого диэлектрика по зависимости E_пр = U / h, где h – толщина диэлектрика, а затем разделить ее E_пр на четыре, предполагая, что запас электрической прочности современной изоляции в четыре раза выше рабочего (номинального) напряжения аппарата U_раб. Найденное значение U_раб по табл. 5.8 как рабочее напряжение аппарата, в котором можно использовать испытуемый диэлектрик. Перечень некоторых диэлектриков приводится в табл. 5.9.