Электротехника \ Техника высоких напряжений

Координация изоляции электрооборудования: Учебное пособие к практическим занятиям, страница 23

чаи, когда интенсивность отказов l является функцией времени a > 1, b > 0. Тогда время безотказной работы х подчиняется распределению Вейбулла, для которого плотность выразится: f(x) = a b x математическое ожидание , дисперсия - b, следовательно, вероятность безотказной работы за время х (интегральная функция распределения) при это равна F(x) = 1 -

Вид распределения Вейбулла по рис. 5.4.

f(x)

a=4

a=2

a=1

0 ( x

Рис. 5.4. Распределение Вейбулла для случайных величин

РАСПРЕДЕЛЕНИЕ ПИРСОНА (распределение c²). Если имется r независимых нормально распределенных случайных величин Y₁,Y₂, , Y_r, параметры которых равны m₁ =0, s то случайная величина Х = c² = распеделена по закону Питерсона , когда

Снижение пробивных напряжений можно оценить по U_0,5 – это напряжение соответствует вероятности 0,5, т.е. является функцией распределения: F(U_0,5) = 0,5. Полагая, что в (5.44) U = U_{0,5 n} и Fn(U_0,5n ) = 0,5, получим,

F₁(U_0,5n) = 1 - , (5.46)

откуда по заданной кривой F₁(U) можно найти значение U_0,5n. Если принять, что F1(U) имеет нормальный закон распределения с параметрами пр1 = U0,5 1 и s1, тогда Fn(U) определяется по (5.44) с учетом (5.41) как

F_n(U) = 1 - 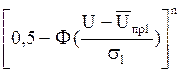. (5.47)

Функция распределения (5.47) не является нормальной и стремится с увеличением n к функции экстремального распределения первого типа с двойным показателем: P(h_nmin) < x) = 1 - при х < 0; P(h_nmax) < x) = , при x > 0, где y = a (x-q), a > 0 и q – параметры распределения. Однако, в качестве первого приближения в окрестнстиU_0,5_n в пределах примерно ± 2sn можно принять функцию F_n(U) нормальной. Тогда с учетом U_0,5n = _пр_n и (5.47) получим

0,5 – Ф(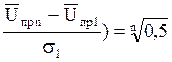

или Ф(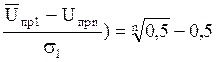. (5.48)

Обозначим в скобках при Ф через a_n, тогда, задаваясь различными

плотность распределения выражается f(x) = 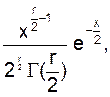при х ³ 0 матожидание - r, а дисперсия -.2r. Число слагаемых r называется числом степени свободы. С ростом r распределение Пирсона приближается к нормальному закону, так как при этом коэффициенты асимметрии и эксцесса стремятся к нулю.

Применение распределения Пирсона.

1. Это может быть распределением некоторых случайных физических явлений, например, распределение молекул газа по кинетическим энергиям с числом свободы r = 3.

2. Чаще это распределение используется при статистической обработке опытных данных, когда так называемым “критерием Пирсона” или “критерием c² “ характеризуют вероятность появления случайной величины большей c (см. подраздел 5.2).