Координация изоляции электрооборудования: Учебное пособие к практическим занятиям, страница 35

63

Снижение пробивных напряжений можно оценить по U_0,5 – это напряжение соответствует вероятности 0,5, т.е. является функцией распределения: F(U_0,5) = 0,5. Полагая, что в (5.44) U = U_{0,5 n} и Fn(U_0,5n ) = 0,5, получим,

                             F₁(U_0,5n) = 1 - ,                               (5.46)

откуда по заданной кривой F₁(U) можно найти значение U_0,5n. Если принять, что F1(U) имеет нормальный закон распределения с параметрами пр1 = U0,5 1 и s1, тогда Fn(U) определяется по (5.44) с учетом (5.41) как

                     F_n(U) = 1 - 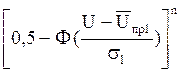.                   (5.47)

Функция распределения (5.47) не является нормальной и стремится с увеличением n к функции экстремального распределения первого типа с двойным показателем: P(h_nmin) < x) = 1 - при х < 0; P(h_nmax) < x) = , при x > 0, где y = a (x-q), a > 0 и q – параметры распределения. Однако, в качестве первого приближения  в окрестнстиU_0,5n в пределах примерно ± 2sn можно принять функцию F_n(U) нормальной. Тогда с учетом U_0,5n = _{пр n} и (5.47) получим

0,5 – Ф(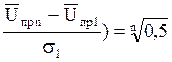

или                          Ф(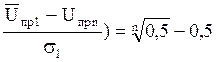.                      (5.48)

Обозначим в скобках при Ф через a_n, тогда, задаваясь различными

64

величинами  n, можно вычислить Ф(a_n) =  и определить по таблице нормального закона a_n = arg - эта зависимость приведена в табл. 5.10.

Таблица 5.10

Зависимости a_n и b_n от числа элементов в изделии