t1 – время нарастания приложенного к промежутку напряжения до величины, когда выполняется условие самостоятельности разряда;
tс – время ожидания начального эффективного электрона, которое называется статистическим временем запаздывания;
tj - время формирования разряда, необходимое для полного пробоя промежутка.
Тогда полное время запаздывания разряда окажется:
tp = t1 + tc + tj . (5.32)
tc и tj носят статистический характер, поскольку на возникно
52
тически не зависит от вида F(x) и от числа опытов n, а зависит только от числа разрядов k. Закон распределения случайной величины U при увеличении n приближается к распределению c2.Поэтому меру расхождения U обычно обозначают c2.
Если учесть, что 
, то
(5.20)
Число степеней свободы r распределения c2 определяется числом разрядов k минус число независимых условий (связей), наложенных на 
. Число связей определяется
следующими условиями:
1. Условия нормировки должны выполняться как для теоретического, так и для статистических распределений.
2. Совпадение теоретических и статистических числовых характеристик. Таким образом, число степеней свободы
r = k – (
+ 1),
(5.21)
где k –
число разрядов, - число совпадающих
числовых характеристик теоретического статистического распределений. Так, если
принимаются равными первые два момента mx » 
и Dx » 
, что полностью описывает
симметричные распределения, то r = k – 3.
Схема применения критерия Пирсона следующая.
1. Составляется сгруппированный статистический ряд; число разрядов должно быть порядка k » 10, а в каждом разряде должно быть не менее mi = 5 – 8 значений переменной Х, так как применение критерия Пирсона справедливо при числе измерений n > 50 – 60.
45
Коэффициент ударной ионизации a имеет большое значение для анализа закономерностей возникновения и развития электрического разряда в газе. Для начала разряда необходим хотя бы один свободный электрон, обладающий энергией, достаточной для ионизации нейтральной молекулы – это эффективный электрон. После первого акта ионизации происходит каскад ионизаций, образуется поток лавин постепенно увеличивающегося числа электронов. Их число в лавине определится соотношением
,
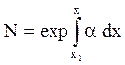(5.30) в котором х1 – координата появления начального
эффективного электрона, а (х – х1) – путь, пройденный лавиной по силовой
линии электрического поля.
В процессе развития лавины, кроме новых электронов, образуются положительные ионы и фотоны. Их воздействие на катод и фотоионизация в объеме газа приводит к появлению так называемых вторичных электронов, общее число которых Ne = g (N - 1), причем коэффициент пропорциональности g - это коэффициент вторичной ионизации. Начальный электрон появляется за счет внешнего ионизатора. Для дальнейшего развития разряда необходимо, чтобы начальная лавина с помощью вторичных процессов ионизации создала хотя бы один вторичный эффективный электрон, который положил бы начало новой лавине. Это условие самостоятельности разряда и записывается как Ne ³ 1 или c учетом (5.30) в виде
51
2. Подсчитывается числовая характеристика распределения.
3. Рассчитываются по оценкам числовых характеристик теоретические вероятности Pi попадания в интервал xi-1, xi. Так, например, для нормального закона
(5.22)
для закона равномерной плотности
(5.23)
4. Вычисляется c2.
5. Определяется число степеней свободы r –k – ( + 1) - большей частью + 1 = 3.
6. Задается уровень значимости a1.
7. Используя табл. 5.6, по a1 и r определяется граничное значение 
.
8. Сравниваются c2
и ; если c2 >,
то гипотеза о соответствии 
и F(x) отвергается c данным уровнем значимости a1, в противном случае гипотеза принимается.
ЗАДАЧА 3. В задаче 1 проверить соответствие эмпирического распределения закону равномерности плотности по критерию c2.
РЕШЕНИЕ. Вычисление опытной меры расхождения c2 сведено в табл. 5.7. Поясним расчеты
теоретических вероятностей Pi . Для 1-го интервала 
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.