Координация изоляции электрооборудования: Учебное пособие к практическим занятиям, страница 33

деление задается некоторой функцией с плотностью вероятности f(W). Для отыскание вероятности ионизации газа одним электроном применим формулу полной вероятности Р(А) = . Гипотезы H_i в данном случае состоит в том, что энергия электрона W больше энергии ионизации W_и, их вероятности равны f(W) dW. Вероятности P(A/H_i) равны вероятностям ионизации р_и(W) при условии, что W > W_и . В результате вероятность ионизации определится как 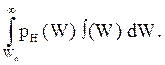 Умножив эту вероятность на среднее число соударений электронов с молекулами газа, определяем коэффициент ударной ионизации:

a = 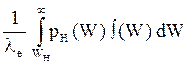.                      (5.24)

Доведем решение задачи до аналитического выражения, устанавливающего связь коэффициента a с параметрами газа и напряженности электрического поля Е. При этом сделаем некоторые допущения. Будем считать, что вероятность р_и(W) имеет следующий вид:

ì  0     при  W < W_и

p_и(W) =   í                                                          (5.25)

î 1     при  W > W_и .

Примем, что распределение электронов подчиняется экспоненциальному закону, как и распределение электронов по длинам свободного пробега, и что электрон набирает энергию W за несколько свободных пробегов  При этом  W =m e E x,  W_ср = m e E l_e,

49

Для остальных интервалов  где i = 2, 3,     , 7. Применим теперь критерий согласия Пирсона при уровне значимости  a₁ = 0,1. имеем   c² = 24,05; k = 8; r = 8 – 3 = 5. По табл. 5.6 находим, что вероятности a₁ = 0,1 при r = 5 соответствует граничное значение  = 9,24. Поэтому  c² > , т.е. критерий Пирсона гипотезу о равномерном законе

5.3. ВЕРОЯТНОСТНЫЕ ЗАДАЧИ

КОЭФФИЦИЕНТ УДАРНОЙ ИОНИЗАЦИИ ГАЗА. Важнейшей характеристикой электрического разряда в газе является коэффициент ударной ионизации a, т.е. число ионизаций, совершаемых одним электроном на пути в 1 см по направлению силовых линий электрического поля в промежутке. Среднее число соударений электронов с нейтральными молекулами газа равно 1 / l _е, где l _е – средняя длина свободного пробега электрона. Столкновения электронов могут быть упругими и неупругими, причем ионизирующими будут неупругие столкновения тех электронов, которые обладают энергией, равной или большей энергии ионизации нейтральных молекул W_и.

Вероятность ионизации при столкновении P_и(W) является функцией энергии электрона W. Она равна нулю при энергиях электрона меньших W_и, затем возрастает, проходит через максимум и уменьшается при дальнейшем возрастании энергии. С другой стороны, электроны двигаясь в электрическом поле, обладают различными энергиями W, их распре

48

деление задается некоторой функцией с плотностью вероятности f(W). Для отыскание вероятности ионизации газа одним электроном применим формулу полной вероятности Р(А) = . Гипотезы H_i в данном случае состоит в том, что энергия электрона W больше энергии ионизации W_и, их вероятности равны f(W) dW. Вероятности P(A/H_i) равны вероятностям ионизации р_и(W) при условии, что W > W_и . 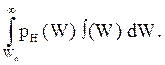В результате вероятность ионизации определится как  Умножив эту вероятность на среднее число соударений электронов с молекулами газа, определяем коэффициент ударной ионизации:

a = 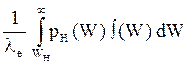.                      (5.24)

Доведем решение задачи до аналитического выражения, устанавливающего связь коэффициента a с параметрами газа и напряженности электрического поля Е. При этом сделаем некоторые допущения. Будем считать, что вероятность р_и(W) имеет следующий вид:

ì  0     при  W < W_и

p_и(W) =   í                                                          (5.25)

î 1     при  W > W_и .

Примем, что распределение электронов подчиняется экспоненциальному закону, как и распределение электронов по длинам свободного пробега, и что электрон набирает энергию W за несколько свободных пробегов  При этом  W =m e E x,  W_ср = m e E l_e,

49

ниям, т.е. характеризуют пробои ослабленных мест в изоляционной конструкции. Тогда согласно (5.45) вероятность пробоя одного из n ослабленных мест определяется суммированием вероятностей пробоя каждого этого места.