Координация изоляции электрооборудования: Учебное пособие к практическим занятиям, страница 20

u_оп = R i_м + L , где L = L₀ h. Для упрощения задачи, что потенциал на проводе равен нулю, т.е. напряжение u_оп равно напряжению u_и  , приложенному к изоляции гирлянды. Пусть ток молнии имеет расчетную форму по рис. 6.1 с амплитудой I_м и крутизной a_м. Тогда максимальное значение напряжения на гирлянде равно графику рис. 6.4, где  U_иmax = R I_м + L a_м. Условие пробоя изоляции определяется неравенством R Iм + L a_м ³ U_i или a_м ³ .

69

Заметим, что в разных книгах и справочниках под одним и тем же термином “интеграл вероятности” понимают определение (5.7) и две его модификации: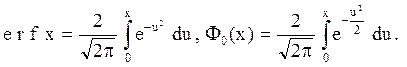

Поэтому прежде, чем пользоваться таблицами интеграла вероятности, следует обратить внимание на принятое определение.

Связь между модификациями интеграла вероятности следующая:

Ф(х) = Ф₀(х),     Ф(х) =

Вероятность попадания случайной величины на интервал ( х₁, х₂ ) в соответствии с Р(a £ Х < b) = F(b) – F(a) и (5.8) равна

Р(х₁ < Х < х₂) = Ф() – Ф() .                      (5.9)

В (5.9) важно, что вероятность попадания на интервал (m - b, m + b),т.е. вероятность отклонения от математического ожидания  m  не более, чем на ± b , равна

Р(|Х - m| < b  = Ф() = 2 Ф(b).                  (5.10)

Вычисления при различных значениях b сведены в табл. 5.2.

Таблица 5.2

Отклонение от среднего значений b

28

где k – порядковый номер случайной величины х_max в вариационном ряду, в котором все N значений случайной величины расположены в порядке возрастания, а уравнение выравнивающей прямой х_max = , где  и  - параметры распределения линейной связи y = a (x – q), если a > 0 , найдено на основании обработки статистического ряда. Получаются следующие результаты:  Ожидаемое максимальное значение I_м на уровне 5 % значимости с доверительными вероятностями 0,99 и 0,999 оказались равными 52,5 и 76,5 кА.

            6.2. ПРОБОЙ ИЗОЛЯЦИИ ПРИ ПУМ .

Рассмотрим ПУМ в заземленную металлическую или железобетонную конструкцию электроустановки, например в вершину опоры ЛЭП, в вершину молниеотвода, установленного на портале открытого распределительного устройства (ОРУ) подстанции или станции и т.п. по рис. 6.2.

Заземляющее устройство обладает некоторым активным соп-ротивлением R, а индуктивность  металлической конструкции опоры на единицу длины – L (активное сопротвление опоры из-за его малости не учитывается). На высоте h на опоре установлена гирлянда изоляторов, поддерживающая провод, импульсная электрическая прочность которой известна и равна U_i. Требуется определить вероятность пробоя изоляции или вероят вероятность того, что максимальное

68

Таким образом, отклонение от среднего, превышающее 3, маловероятно – Р(|Х-m|) = 0,0027. Поэтому обратное неравенство практически достоверно. Часто эго свойство нормального распределения называют правилом “трех сигм”. Использовать нормальный закон распределения как удобный для расчетов можно  только после оценки вероятностей нефизических выводов.

УСЕЧЕННОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ. В технических задачах часто встречаются случайные величины, имеющие ограниченный диапазон изменения  a £ Х £ b. Например, в задачах о координации изоляции, когда кратность перенапряжений  k лежит в пределах 1 £ k < , разрядные напряжения всегда положительны 0 < U < ¥. В то же время внутри заданного  диапазона (a, b) распределение случайной величины хорошо аппроксимируется нормальным законом ¦(х) по (5.4).Тогда для приближенного описания реальных случайных величин используют “усеченный нормальный закон”.

ó      0,         х < a или х > b,

¦_ус(х) = í                                                                       (5.11)

î