Координация изоляции электрооборудования: Учебное пособие к практическим занятиям, страница 25

Таблица 5.8

Рабочие напряжения аппаратов

Таблица 5.9

Диэлектрики и их электрические характеристики

61

дискретных случайных величин согласно формуле Бернулли Р_n(m) =  = C называется биноминальным, так как вероятность Р_n(m) по форме представляет собой член разложения бинома (р + q). Тогда при описании исходов серии из n повторяющихся независимых испытаний найдем числовые характеристики.

Математическое ожидание дискретной случайной величины Х – число благоприятных исходов испытаний, принимающее значение m = 0, 1,   , n, согласно определению m_k = равно

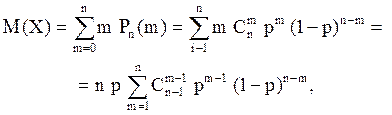
так как m C

Cумма равна

 так что                                   М(Х) =n p.                                         (5.14)

Дисперсия расчитывается : D(X) = M(X(X-1)) = M(X)(M(X)-1:

                                          D(X) = n p(1-p).                                     (5.15)

Коэффициент асиметриии равен S_k =  коэффициент эксцесса где q = 1 – p. При увеличении числа наблю-

36

ниям, т.е. характеризуют пробои ослабленных мест в изоляционной конструкции. Тогда согласно (5.45) вероятность пробоя одного из n ослабленных мест определяется суммированием вероятностей пробоя каждого этого места.

Из (5.43) – (5.45) следует, что зависимость вероятности пробоя изоляции конструкции в целом смещена в сторону меньших значений напряжения по сравнению с аналогично зависимостью для одного элемента, кроме того, уменьшаются разбросы в пробивных напряжениях (см. рис.5.11).

                             F(U)

                     1,0

0,5                         1              2

                    0,1                                                           U

                                       U_min  

Рис. 5.11. Вероятности пробоя изоляционной конструкции 1

 и ее элемента 2

Обычно, электрический пробой при одной и той же толщине твердого диэлектрика подчиняется статистическим закономерностям и имеет значительный разброс дискретных значений пробивного напряжения. Для построения  интегральной кривой 2 по рис. 5.11 все дискретные значения пробивных напряжений располагают в возрастающий ряд чисел и задают каждому из них вероятность появления случайного числа (пробивного напряжения), а затем анализируют появление  пробивного напряжения U с той или иной вероятностью. Так, вероятность появления минимального напряжения говорит о явном

60

дений n  ¥ , биноминальное распределение Р_n(m) =                           = C, как следует из теоремы Муавра-Лапласа, стремится к нормальному закону с параметрами (5.14), (5.15). Прак-тически уже для n > 50 погрешность приближения становится небольшой. Аппроксимация биноминального распределения нормальным имеет большое практическое значение, так как существенно упрощаются вычисления. Часто в качестве случайной величины рассматривается статистическая вероятность (частность)  появления события n независимых испытаниях. Тогда из (5.14), (5.15) имеем

                               ì

î                                (5.16)

Таблицы биноминальнго распределения приведены в /2/.